题目内容
9.如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在AC上,点E在AC上.(1)证明:DE∥BC.
(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判断AC与MN的位置关系,并说明理由.
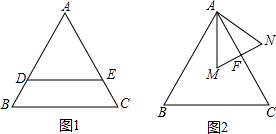
分析 (1)根据两个图形必须是相似形得到∠ADE=∠B,根据平行线的性质证明即可;
(2)延长AM交BC于D,根据等腰三角形三线合一得到∠DAC=30°,求出∠AFM=90°,得到答案.
解答 (1)证明:∵△ADE是△ABC的位似图形,
∴△ADE∽△ABC,
∴∠ADE=∠B,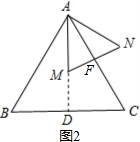
∴DE∥BC;
(2)AC⊥MN.
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN.
点评 本题考查的是位似变换的性质、旋转变换以及等边三角形的性质,掌握两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形是解题的关键.

练习册系列答案
相关题目
19.计算($\frac{1}{3}$)-1的结果为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
20. 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD. 我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达11公里处.
我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达11公里处.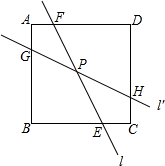 如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$.
如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$.