题目内容
5. 在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
分析 由以原点O为位似中心,位似比为1:2,把△ABO缩小,直接利用位似图形的性质求解即可求得答案.
解答 解:∵以原点O为位似中心,位似比为1:2,把△ABO缩小,B(5,-2),
∴点B的对应点B′的坐标是:($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
故答案为:($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
点评 此题考查了位似图形的性质.注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
相关题目
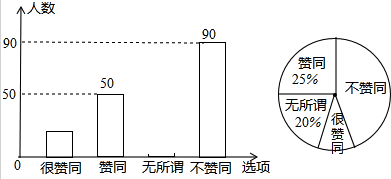
13.纳米是一种长度单位,1纳米=10-9米,已知某种植物花粉的直径约为15000纳米,那么用科学记数法表示该种花粉的直径为( )
| A. | 1.5×10-13米 | B. | 15×10-6米 | C. | 1.5×10-5米 | D. | 1.5×10-6米 |
20. 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
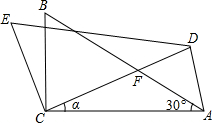 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.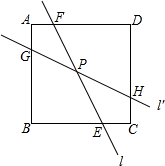 如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$.
如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$.