题目内容
19.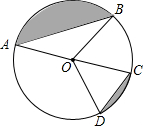 如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)
如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)
分析 易得弧AB,CD是一个半圆弧,我们将C点转到与A点重合处,那么O、B、D′就在一条直线上,而且是一直径,所以阴影部分的面积=半圆的面积-一个直角三角形的面积,然后依面积公式计算即可.
解答  解:延长BO交⊙O于D′,连接AD′,
解:延长BO交⊙O于D′,连接AD′,
∵$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,
∴弧AB,CD就是一个半圆弧,
则B、O、D′就在一条直线上,而且BD′是一直径,
∴∠D′AB=90°,弧AD′=弧CD,
∴AD′=CD=4,
在Rt△CAB中,由勾股定理得:BD′=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴OB=2$\sqrt{5}$,
∴阴影部分的面积=$\frac{1}{2}$S⊙O-S△D′AB
=π×(2$\sqrt{5}$)2×$\frac{1}{2}$-$\frac{1}{2}$×4×8
=15.4.
故答案为:15.4.
点评 本题的关键是作辅助线,从图中看出阴影部分的面积=半圆的面积-一个直角三角形的面积.

练习册系列答案
相关题目
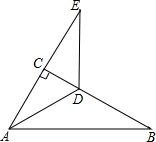 如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
 已知CD平分∠ACB,DE∥AC,求证:DE=BC.
已知CD平分∠ACB,DE∥AC,求证:DE=BC.