题目内容
10.设y=$\frac{ax+b}{cx+d}$,a,b,c,d都是有理数,x是无理数,求证:(1)当bc=ad时,y是有理数.
(2)当bd≠ad时,y是无理数.
分析 (1)把y=$\frac{ax+b}{cx+d}$变形,再由bc=ad,得出(cx+d)(cy-a)=0,根据分式有意义的条件,从而得出y是有理数;
(2)把y=$\frac{ax+b}{cx+d}$变形,再由bc≠ad,以及a,b,c,d都是有理数,x是无理数,得出y为无理数.
解答 解:(1)∵bc=ad,
∴b=$\frac{ad}{c}$,
∵y=$\frac{ax+b}{cx+d}$,
∴xcy+dy=ax+$\frac{ad}{c}$,
∴c2xy+cdy-acx-ad=0,
∴cx(cy-a)+d(cy-a)=0,
∴(cx+d)(cy-a)=0,
∵cx+d≠0(分母不为0),
∴cy-a=0,
∵a,c为有理数,
∴y为有理数;
(2)∵y=$\frac{ax+b}{cx+d}$,
∴xcy+dy=ax+b,
∴x=$\frac{b-dy}{cy-a}$,
∵x为无理数,a,b,c,d都是有理数,
∴y为无理数.
点评 本题考查了实数,以及它的分类,证明一个数是有理数或无理数是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.下列方程中,是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | x2+3x-1=0 | C. | ax2+bx+c | D. | 3x+y=10 |
 在下面五环相交把五环分成9个部分,在这9个的部分填入1-9,使得5个五环内的数字和恰好构成5个公差为2的等差数列,给出一种填法.
在下面五环相交把五环分成9个部分,在这9个的部分填入1-9,使得5个五环内的数字和恰好构成5个公差为2的等差数列,给出一种填法.
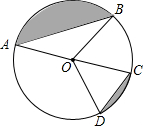 如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)
如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)