题目内容
9.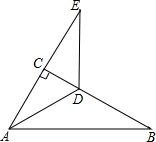 如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.
分析 (1)由直角三角形的性质和角平分线得出∠DAB=∠ABC,得出DA=DB,再由线段垂直平分线的性质得出DE=DA,即可得出结论;
(2)由线段垂直平分线的性质得出BA=BE,再由∠CAB=60°,即可得出△ABE是等边三角形.
解答 (1)证明:∵∠ACB=90°,∠ABC=30°,
∴BC⊥AE,∠CAB=60°,
∵AD平分∠CAB,
∴∠DAB=$\frac{1}{2}$∠CAB=30°=∠ABC,
∴DA=DB,
∵CE=AC,
∴BC是线段AE的垂直平分线,
∴DE=DA,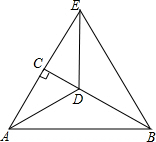
∴DE=DB;
(2)△ABE是等边三角形;理由如下:
连接BE,如图:
∵BC是线段AE的垂直平分线,
∴BA=BE,
即△ABE是等腰三角形,
又∵∠CAB=60°,
∴△ABE是等边三角形.
点评 本题考查了等边三角形的判定方法、线段垂直平分线的性质、等腰三角形的判定等知识;本题综合性强,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列方程中,是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | x2+3x-1=0 | C. | ax2+bx+c | D. | 3x+y=10 |
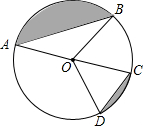 如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)
如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)