题目内容
20.已知2m•2m•8=211,则m=4.分析 将已知中的2m•2m•8化为同底数的幂,然后利用同底数幂的乘法法则进行计算,再根据指数相同列式求解即可.
解答 解:2m•2m•8=2m•2m•23=2m+m+3,
∵2m•2m•8=211,
∴m+m+3=11,
解得m=4.
故答案为4.
点评 本题考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即am•an=a m+n(m,n是正整数),运用同底数幂的乘法法则时需要注意:
(1)三个或三个以上同底数幂相乘时,也具有这一性质:am•an•ap=am+n+p(m、n、p均为正整数);
(2)公式的特点:左边是两个或两个以上的同底数幂相乘,右边是一个幂指数相加.

练习册系列答案
相关题目
11.计算$\frac{1}{x-1}$÷$\frac{x}{{x}^{2}-1}$的结果是( )
| A. | 1 | B. | x+1 | C. | $\frac{x+1}{x}$ | D. | $\frac{1}{x-1}$ |
8.掷一枚质地均匀的硬币5次,下列说法正确的是( )
| A. | 必有5次正面朝上 | B. | 掷2次必有1次正面朝上 | ||
| C. | 不可能5次正面朝上 | D. | 可能有2次正面朝上 |
5.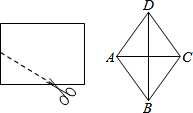 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )| A. | 10 | B. | 20 | C. | 40 | D. | 80 |
12.已知方程组$\left\{\begin{array}{l}{5x+y=3}\\{ax+5y=4}\end{array}\right.$和$\left\{\begin{array}{l}{x-2y=5}\\{5x+by=1}\end{array}\right.$有相同的解,则a,b的值为( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-4}\\{b=-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-6}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=14}\\{b=2}\end{array}\right.$ |
10.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | x2+y2=(x+y)(x-y) | C. | (a+4)(a-4)=a2-16 | D. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 |
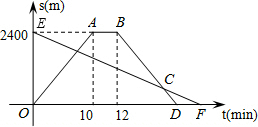 小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.
小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.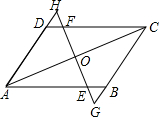 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.