题目内容
2.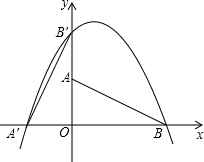 如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.
如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)M为x轴上一点,MN∥A′B′交抛物线于点N,以A′、B′、M、N为顶点的四边形是平行四边形,试求M点的坐标;
(3)P为线段AB上一点,PQ∥y轴,交抛物线于点Q,四边形B′OPQ为等腰梯形,直接写出点P的坐标.
分析 (1)由旋转的性质可知点A′(-1,0),B′(0,2),然后根据待定系数法求得抛物线的解析式即可;
(2)由四边形A′、B′、M、N为平行四边形可知:B′N∥x轴,B′N=A′M,从而可知点N的纵坐标为2,然后将y=2代入抛物线的解析式可求得点N的坐标,然后根据B′NA′M=1,即可求得点M的坐标为(0,0);
(3)利用待定系数法线求得直线AB的坐标,然后设点P的横坐标为m,可得到点P的坐标为(m,$-\frac{1}{2}m+1$),点Q的坐标为(m,-m2+m+2),然后根据梯形为等腰梯形可知点P与点Q关于y=1对称,然后列出关于m的方程求得m的值,从而可得到点P的坐标.
解答 解:(1)由旋转的性质可知:点A′(-1,0),B′(0,2),
设抛物线的解析式为y=a(x+1)(x-2),
将x=0,y=2代入函数的解析式得:2=a×1×(-2),
解得:a=-1,
∴抛物线得解析式为y=-x2+x+2;
(2)如图1所示: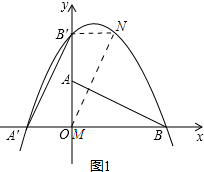
∵四边形A′、B′、M、N为平行四边形,
∴B′N∥x轴,B′N=A′M
∴点B′与点N的纵坐标相等.
将y=2代入抛物线的解析式得:-x2+x+2=2,
解得:x=0,x=1,
∴B′N=1.
∴A′M=1.
∴点M的坐标为(0,0);
(3)如图2所示: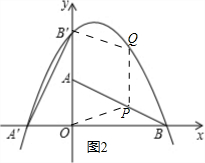
设直线AB的解析式为y=kx+b,
将A(0,1),B(2,0)代入得:$\left\{\begin{array}{l}{b=1}\\{2k+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=1}\\{k=-\frac{1}{2}}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{1}{2}$x+1,
设点P的坐标为(m,$-\frac{1}{2}m+1$),则点Q的坐标为(m,-m2+m+2)
∵四边形为等腰梯形,
∴点P与点Q关于y=1对称.
∴-$\frac{1}{2}m+1-{m}^{2}+m+2$=2.
解得:${m}_{1}=\frac{-\sqrt{17}+1}{4}$(舍去),${m}_{2}=\frac{\sqrt{17}+1}{4}$,
将${m}_{2}=\frac{\sqrt{17}+1}{4}$代入$-\frac{1}{2}m+1$得:$-\frac{1}{2}m+1$=$\frac{7-\sqrt{17}}{8}$.
∴点P得坐标为($\frac{\sqrt{17}+1}{4}$,$\frac{7-\sqrt{17}}{8}$).
点评 本题主要考查的是二次函数的综合应用,根据旋转的性质、平行四边形的性质以及等腰梯形的特点找出关键点的坐标之间的关系是解题的关键.

| A. | 6,6 | B. | 6,8 | C. | 7,6 | D. | 7,8 |
| A. | 4 | B. | 12 | C. | 24 | D. | 28 |
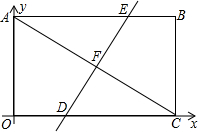 如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,
如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4, 如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.
如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.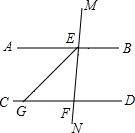 如图,AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEN交CD于点G.若∠MEB=80°,求∠EGD的度数.
如图,AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEN交CD于点G.若∠MEB=80°,求∠EGD的度数.