题目内容
6.已知x=$\frac{1}{\sqrt{2}+1}$,y=$\frac{1}{\sqrt{2}-1}$,求$\frac{{x}^{3}-{x}^{2}y+x{y}^{2}-{y}^{3}}{x-y}$的值.分析 由x=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,y=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,进一步化简分式代入球的答案即可.
解答 解:∵x=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,y=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,
∴$\frac{{x}^{3}-{x}^{2}y+x{y}^{2}-{y}^{3}}{x-y}$
=$\frac{{x}^{2}(x-y)+{y}^{2}(x-y)}{x-y}$
=x2+y2
=3-2$\sqrt{2}$+3+2$\sqrt{2}$
=6.
点评 此题考查二次根式的化简求值,注意先化简二次根式和分式,再进一步代入求得答案即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.代数式$\frac{\sqrt{x-5}}{x-6}$有意义,则x的取值范围是( )
| A. | x≤5 | B. | x≥5 | C. | x>5且x≠6 | D. | x≥5且x≠6 |
7.如果mn<0,且m<0,则点P(m2,n-m)在( )
| A. | 笫一象限 | B. | 笫二象限 | C. | 笫三象限 | D. | 笫四象限 |
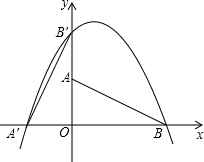 如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.
如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.