题目内容
2.在Rt△ABC中,∠C=90°,∠A=30°,求证:AC2=3BC2.分析 延长BC到D,使CD=BC,连接AD,可证明△ACB≌△ACD,进而可以证明△ABD是等边三角形,即可得到BC的AB的关系,再利用勾股定理即可证明AC2=3BC2.
解答 证明:延长BC到D,使CD=BC,连接AD.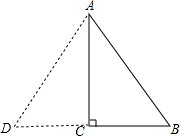
∵∠ACB=90°,
∴∠ACD=90°.
在△ACB和△ACD中,
$\left\{\begin{array}{l}{AC=AC}\\{∠ACD=∠ACB}\\{BC=DC}\end{array}\right.$
∴△ACB≌△ACD(SAS).
∴AB=AD.
∵∠A=30°
∴∠BAC=60°.
∴△ABD为等边三角形
∴AB=AD=BD,
∴BC=$\frac{1}{2}$AB,
∴AB=2BC,
∵AC2+BC2=AB2,
∴AC2=3BC2.
点评 本题考查了勾股定理的运用以及30度角的直角三角形,根据题意构造等腰三角形,进而利用等腰三角形的性质解答.此题关键是作辅助线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.某商场用18万元购进A、B两种商品,其进价和售价如下表:
(1)若销售完后共获利3万元,该商场购进A、B两种商品各多少件;
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
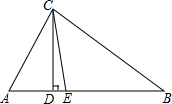 如图,在Rt△ABC中,CD为斜边AB上的高,且AD=2厘米,BD=8厘米,求:
如图,在Rt△ABC中,CD为斜边AB上的高,且AD=2厘米,BD=8厘米,求: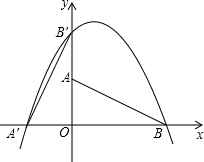 如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.
如图,直角坐标系中Rt△ABO,其顶点为A(0,1)、B(2,0)、O(0,0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.