题目内容
13.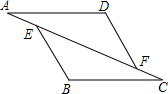 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC,若AD+BC=10,则AD的长是( )
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC,若AD+BC=10,则AD的长是( )| A. | 3 | B. | 4 | C. | 6 | D. | 5 |
分析 根据题意,可以得到△ADF≌△CBE,从而可以得到AD与BC的关系,由AD+BC=10,从而可以求得AD的长,本题得以解决.
解答 解:∵点A、E、F、C在同一直线上,AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠D=∠B}\\{AF=CE}\end{array}\right.$
∴△ADF≌△CBE(AAS),
∴AD=CB,
∵AD+BC=10,
∴AD=BC=5,
故选D.
点评 本题考查全等三角形的判定与性质,解答此类问题的关键是明确题意,证明出△ADF≌△CBE.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
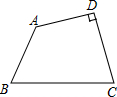 如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.
如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.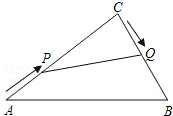 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求: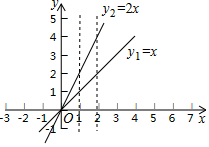 小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题:
小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题: 如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.
如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.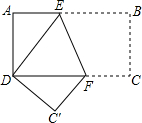 在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.
在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.