题目内容
18. 如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.
如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.
分析 连接OA,根据垂径定理求出AB=2AM,已知OA、OM,根据勾股定理求出AM即可.
解答 解:连接OA,
∵⊙O的直径CD=20cm,
∴OA=10cm,
在Rt△OAM中,由勾股定理得:AM=$\sqrt{1{0}^{2}-{6}^{2}}$=8cm,
∴由垂径定理得:AB=2AM=16cm.
故答案为:16.
点评 本题考查了垂径定理和勾股定理的应用,关键是构造直角三角形.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
7.下列图形一定是轴对称图形的是( )
| A. | 直角三角形 | B. | 平行四边形 | C. | 直角梯形 | D. | 正方形 |
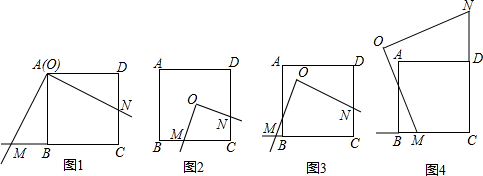
 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )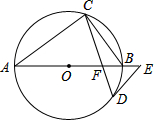 如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC.
如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC. 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( ) 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.