题目内容
20.△ABC的两条高AD,BE交于点H,若BH=AC,则∠ABC=( )| A. | 60° | B. | 45° | C. | 60°或120° | D. | 45°或135° |
分析 根据题意画出两个图形,证△HBD≌△CAD,推出AD=DB,推出∠DAB=∠DBA,根据三角形内角和定理和等腰三角形的性质求出∠ABD,即可求出答案.
解答 解:分为两种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠∠BEC=90°,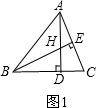
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中,
$\left\{\begin{array}{l}{∠HBD=∠CAD}\\{∠BDH=∠ADC=90°}\\{BH=AC}\end{array}\right.$,
∴△HBD≌△CAD(AAS),
∴BD=AD,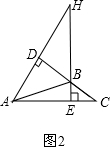
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
$\left\{\begin{array}{l}{∠HDB=∠ADC}\\{∠H=∠C}\\{BH=AC}\end{array}\right.$,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°-45°=135°;
故选:D.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,垂直定义,三角形的内角和定理等知识点的应用,用了分类讨论思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若函数y=k1x(k1≠0)和函数y=$\frac{{k}_{2}}{x}$(k2≠0)在同一坐标系内的图象没有公共点,则k1和k2( )
| A. | 互为倒数 | B. | 符号相同 | C. | 绝对值相等 | D. | 符号相反 |
 如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.
如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.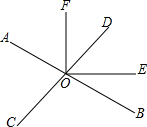 如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11
如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11