题目内容
5．已知抛物线y=2x2-8x+1的顶点为C，且直线y=-kx-3经过点C，则直线与两坐标轴所围成的三角形的面积为$\frac{9}{4}$．分析 首先利用配方法求出抛物线顶点C的坐标，然后求出k的值，进而求出直线与两坐标轴所围成的三角形的面积．
解答 解：∵抛物线解析式为y=2x2-8x+1，
∴y=2（x-2）2-7，
∴顶点C坐标为（2，-7），
∵直线y=-kx-3经过点C，
∴-7=-2k-3，
∴k=2，
∴直线解析式为y=-2x-3，
令x=0，y=-3，令y=0，x=$\frac{3}{2}$，
∴直线与两坐标轴所围成的三角形的面积为$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$．
故答案为$\frac{9}{4}$．
点评 本题主要考查了二次函数的性质，解答本题的关键是利用配方法求出抛物线的顶点坐标，此题难度一般．
练习册系列答案
名校课堂系列答案
相关题目
17．下列各点中，在反比例函数y=$\frac{3}{x}$图象上的点是（ ）
| A． | （$\frac{1}{3}$，-9） | B． | （3，1） | C． | （-1，3） | D． | （6，-$\frac{1}{2}$） |
20．△ABC的两条高AD，BE交于点H，若BH=AC，则∠ABC=（ ）
| A． | 60° | B． | 45° | C． | 60°或120° | D． | 45°或135° |
如图所示，在△ABC中：
17．
如图，AB为⊙O的直径，C、D是⊙O上的两点，∠CDB=25°，过点C作⊙O的切线交AB的延长线于点E，则∠E的度数为（ ）
如图，AB为⊙O的直径，C、D是⊙O上的两点，∠CDB=25°，过点C作⊙O的切线交AB的延长线于点E，则∠E的度数为（ ）| A． | 40° | B． | 50° | C． | 55° | D． | 60° |
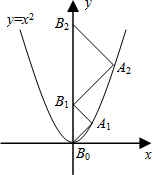如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2015B2014B2015的腰长=2015$\sqrt{2}$．