题目内容
 住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:AB代表小明所处位置到地面的距离,即AB=160米,CD代表“中原第一高楼”,作AE⊥CD于点E,在直角△AEC和直角△ADE中,分别利用三角函数求得EC和DE,即可求解.
解答: 解:如图所示,
解:如图所示,
AB代表小明所处位置到地面的距离,即AB=160米,
CD代表“中原第一高楼”,
作AE⊥CD于点E.
由题意可知,四边形ABDE是矩形,所以AB=DE=160米.
在Rt△ADE中,
∵tan∠DAE=
,DE=160,
∴tan45°=
=1,
∴AE=160.
在Rt△AEC中,
∵tan∠AEC=
,AE=160,
∴tan37°=
=0.75,
∴CE=120,
∴CD=CE+DE=120+160=280(米),
∴“中原第一高楼”高280米.
 解:如图所示,
解:如图所示,AB代表小明所处位置到地面的距离,即AB=160米,
CD代表“中原第一高楼”,
作AE⊥CD于点E.
由题意可知,四边形ABDE是矩形,所以AB=DE=160米.
在Rt△ADE中,
∵tan∠DAE=
| DE |
| AE |
∴tan45°=
| 160 |
| AE |
∴AE=160.
在Rt△AEC中,
∵tan∠AEC=
| CE |
| AE |
∴tan37°=
| CE |
| 160 |
∴CE=120,
∴CD=CE+DE=120+160=280(米),
∴“中原第一高楼”高280米.
点评:此题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于
如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,求救援船航行的速度为多少?
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,求救援船航行的速度为多少? 如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD.
如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD. 如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.
如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长. 如图,直线y=-
如图,直线y=-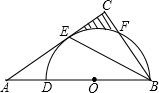 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是