题目内容
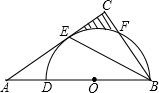 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.(1)求证:AC是⊙O的切线;
(2)已知∠A=30°,⊙O的半径为4,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OE.根据OB=OE得到∠OBE=∠OEB,然后再根据BE是△ABC的角平分线得到∠OEB=∠EBC,从而判定OE∥BC,最后根据∠C=90°得到∠AEO=∠C=90°证得结论AC是⊙O的切线.
(2)连接OF,利用S阴影部分=S梯形OECF-S扇形EOF求解即可.
(2)连接OF,利用S阴影部分=S梯形OECF-S扇形EOF求解即可.
解答: 解:(1)连接OE.
解:(1)连接OE.
∵OB=OE
∴∠OBE=∠OEB
∵BE是∠ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是⊙O的切线;
(2)连接OF.
∵∠A=30°,⊙O的半径为4,
∴AO=2OE=8,
∴AE=4
,∠AOE=60°,
∴AB=12,
∴BC=
AB=6,AC=6
,
∴CE=AC-AE=2
.
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6-4=2,
∴∠EOF=60°.
∴S梯形OECF=
(2+4)×2
=6
.
S扇形EOF=
=
π,
∴S阴影部分=S梯形OECF-S扇形EOF=6
-
π.
 解:(1)连接OE.
解:(1)连接OE.∵OB=OE
∴∠OBE=∠OEB
∵BE是∠ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是⊙O的切线;
(2)连接OF.
∵∠A=30°,⊙O的半径为4,
∴AO=2OE=8,
∴AE=4
| 3 |
∴AB=12,
∴BC=
| 1 |
| 2 |
| 3 |
∴CE=AC-AE=2
| 3 |
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6-4=2,
∴∠EOF=60°.
∴S梯形OECF=
| 1 |
| 2 |
| 3 |
| 3 |
S扇形EOF=
| 60π×42 |
| 360 |
| 8 |
| 3 |
∴S阴影部分=S梯形OECF-S扇形EOF=6
| 3 |
| 8 |
| 3 |
点评:本题考查了切线的判定与性质及扇形面积的计算,解题的关键是连接圆心和切点,利用过切点且垂直于过切点的半径来判定切线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、抛一枚硬币正面朝上的机会与抛一枚图钉钉尖着地的机会一样大 |
| B、为了解汉口火车站某一天中通过的列车车辆数,可采用全面调查的方式进行 |
| C、彩票中奖的机会是1%,买100张一定会中奖 |
| D、中学生小亮,对他所在的那栋住宅楼的家庭进行调查,发现拥有空调的家庭占100%,于是他得出全市拥有空调家庭的百分比为100%的结论 |
 如图,在△ABC中,AB=2 012,AC=2 010,AD为中线,则△ABD与△ACD的周长之差=
如图,在△ABC中,AB=2 012,AC=2 010,AD为中线,则△ABD与△ACD的周长之差= 住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为
如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为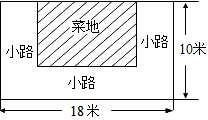 如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地.
如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地.