题目内容
9．计算：（1）2sin45°+（3.14-π）0+$\frac{\sqrt{8}}{2}$；
（2）$\frac{{x}^{2}-1}{x-1}$÷$\frac{{x}^{2}-2x+1}{{x}^{2}-x}$．
分析 （1）原式利用特殊角的三角函数值，零指数幂法则，以及二次根式性质计算即可得到结果；
（2）原式利用除法法则变形，约分即可得到结果．
解答 解：（1）原式=2×$\frac{\sqrt{2}}{2}$+1+$\frac{2\sqrt{2}}{2}$=$\sqrt{2}$+1+$\sqrt{2}$=2$\sqrt{2}$+1；
（2）原式=$\frac{（x+1）（x-1）}{x-1}$•$\frac{x（x-1）}{（x-1）^{2}}$=$\frac{{x}^{2}+x}{x-1}$．
点评 此题考查了分式的乘除法，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
19．下列说法正确的是（ ）
| A． | （3，2）和（2，3）表示同一个点 | B． | 点（$\sqrt{3}$，0）在x轴的正半轴上 | ||
| C． | 点（-2，4）在第四象限 | D． | 点（-3，1）到x轴的距离为3 |
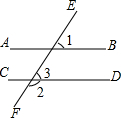如图，已知AB∥CD，∠1=60°，则∠2=120度，∠3=60度．
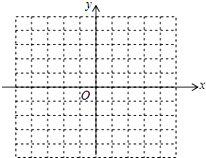在平面直角坐标系中，已知点A（-3，1），B（-1，0），C（-2，-1），请在图中画出△ABC，并画出将△ABC向右平移3个单位得到的△A1B1C1．
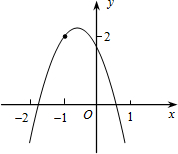如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1、x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：
11．如果点P在x轴正半轴上，则点P的坐标为（ ）
| A． | （0，2） | B． | （-2，0） | C． | （4，0） | D． | （0，-1） |