题目内容
17．
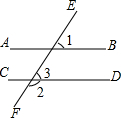如图，已知AB∥CD，∠1=60°，则∠2=120度，∠3=60度．
分析 由AB∥CD，∠1=60°，根据两直线平行，同位角相等，可求得∠3的度数，继而求得∠3的度数．
解答 解：∵AB∥CD，∠1=60°，
∴∠3=∠1=60°，
∴∠2=180°-∠3=120°．
故答案为：120，60．
点评 此题考查了平行线的性质．注意掌握两直线平行，同位角相等定理的应用是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
7．
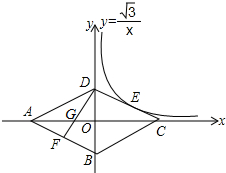如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）
如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）| A． | $\frac{4\sqrt{3}}{3}$ | B． | $\sqrt{3}$+2 | C． | 2$\sqrt{3}$+1 | D． | $\frac{3\sqrt{3}}{2}$+1 |
如图，a∥b，一块等腰直角三角板的直角顶点落在直线b上，一个锐角顶点落在直线a上，若∠1=25°，则∠2=65°．
5．
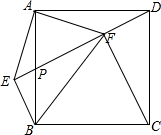如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP的延长线于点E，连接AE，过点A作AF⊥AE，AF交DP于点F，连接BF、CF．下列结论：
①△ABE≌△ADF；②FB=AB；③FC=EF；④BF⊥AF；⑤PF=EP+EB．
其中正确的命题个数有（ ）
如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP的延长线于点E，连接AE，过点A作AF⊥AE，AF交DP于点F，连接BF、CF．下列结论：①△ABE≌△ADF；②FB=AB；③FC=EF；④BF⊥AF；⑤PF=EP+EB．
其中正确的命题个数有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
2．已知二次函数y=x2-2mx+m2+3（m为常数），下列结论正确的是（ ）
| A． | 当m=0时，二次函数图象的顶点坐标为（0，0） | |
| B． | 当m＜0时，二次函数图象的对称轴在y轴右侧 | |
| C． | 若将该函数图象沿y轴向下平移6个单位，则平移后图象与x轴两交点之间的距离为$2\sqrt{3}$ | |
| D． | 设二次函数的图象与y轴交点为A，过A作x轴的平行线，交图象于另一点B，抛物线的顶点为C，则△ABC的面积为m3 |
6．如图图形中，由∠1=∠2能得到AB∥CD的是（ ）
| A． |  | B． |  | ||
| C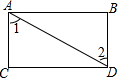． |  | D． |  |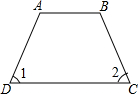
19．若${（{2+y}）^2}+\sqrt{x+y-1}=0$，则xy的值等于（ ）
| A． | -6 | B． | -2 | C． | 2 | D． | 6 |