题目内容
18.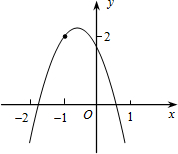 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③abc<0;④b2+8a<4ac.
其中正确的结论有①②.(填写正确结论的序号)
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①根据图象知,当x=-2时,y<0,即4a-2b+c<0;故①正确;
②∵该函数图象的开口向下,
∴a<0;
又∵对称轴-1<x=-$\frac{b}{2a}$<0,
∴2a-b<0,故②正确;
③∵a<0,-$\frac{b}{2a}$<0,
∴b<0.
∵抛物线交y轴与正半轴,
∴c>0.
∴abc>0,故③错误.
④∵y=$\frac{4ac-{b}^{2}}{4a}$>2,a<0,
∴4ac-b2<8a,即b2+8a>4ac,故④错误.
综上所述,正确的结论有①②.
故答案为:①②.
点评 本题主要考查对二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征等知识点的理解和掌握,掌握相关性质是解题的关键.

练习册系列答案
相关题目
6.如图图形中,由∠1=∠2能得到AB∥CD的是( )
| A. | 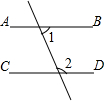 | B. |  | ||
| C. | 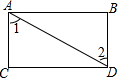 | D. | 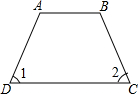 |
3. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.若${({2+y})^2}+\sqrt{x+y-1}=0$,则xy的值等于( )
| A. | -6 | B. | -2 | C. | 2 | D. | 6 |
 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°. 如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.
如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.