题目内容
16. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.
分析 利用圆锥的底面周长等于侧面展开图的扇形弧长,根据弧长公式计算.
解答 解:扇形的弧长是:$\frac{90πR}{180}$=$\frac{πR}{2}$,
圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:$\frac{πR}{2}$=2πr,
即:R=4r,
R与r之间的关系是R=4r.
故答案为:R=4r.
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.下列两个三角形不一定相似的是( )
| A. | 两个等边三角形 | B. | 两个全等三角形 | ||
| C. | 两个等腰直角三角形 | D. | 有一个30°角的两个等腰三角形 |
7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )


| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
5. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
 如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.
如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3. 如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.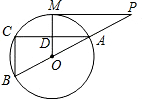 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.