题目内容
14.我们把形如x+$\frac{1}{x}$=m+$\frac{1}{m}$(其中x是未知数,m是常数)的方程称为互为倒数的方程,它的两个解也互为倒数,即x1=m,x2=$\frac{1}{m}$,利用上述结论解下列关于x的方程:(1)2x+$\frac{1}{2x-1}$=$\frac{31}{5}$;
(2)$\frac{{x}^{2}-x+1}{x-1}$=a+$\frac{1}{a-1}$.
分析 根据题中的方法将各方程变形,求出解即可.
解答 解:(1)方程变形得:2x-1+$\frac{1}{2x-1}$=5+$\frac{1}{5}$,
则有2x-1=5或2x-1=$\frac{1}{5}$,
解得:x1=3,x2=$\frac{3}{5}$,
经检验都为分式方程的解;
(2)方程整理得:x+$\frac{1}{x-1}$=a+$\frac{1}{a-1}$,即x-1+$\frac{1}{x-1}$=a-1+$\frac{1}{a-1}$,
则有x-1=a-1或x-1=$\frac{1}{a-1}$,
解得:x1=a,x2=$\frac{a}{a-1}$,
经检验都为分式方程的解.
点评 此题考查了解分式方程,弄清题中的解题方法是解本题的关键.

练习册系列答案
相关题目
4.代数式a+$\frac{1}{2a}$,4xy,$\frac{a+b}{3}$,a,2016,$\frac{1}{2}$a2bc,-$\frac{3mn}{4}$中单项式的个数有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
18.若关于x的方程(k-1)x2-(k-1)x+$\frac{1}{4}$=0有两个相等的实数根,则k的值为( )
| A. | 1 | B. | 2 | C. | 1或2 | D. | 以上都不对 |
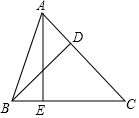 如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC,交BC于E,若BD=8,tan∠CBD=$\frac{3}{4}$,求AC长.
如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC,交BC于E,若BD=8,tan∠CBD=$\frac{3}{4}$,求AC长.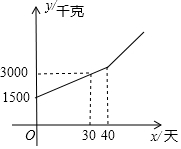 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克. 如图所示,在△ABC中,AB=15,BC=14,S△ABC=84,求tanC的值.
如图所示,在△ABC中,AB=15,BC=14,S△ABC=84,求tanC的值. 已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE.
已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE.