题目内容
2．
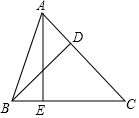如图，D是△ABC的边AC上一点，CD=2AD，AE⊥BC，交BC于E，若BD=8，tan∠CBD=$\frac{3}{4}$，求AC长．
分析 根据已知条件和锐角三角函数的定义求得CD的长度，则AC=AD+CD=$\frac{3}{2}$CD．
解答 解：∵如图，AE⊥BC，BD=8，tan∠CBD=$\frac{3}{4}$，
∴tan∠CBD=$\frac{CD}{BD}$=$\frac{CD}{8}$=$\frac{3}{4}$，
∴CD=6．
∵CD=2AD，
∴AC=AD+CD=$\frac{3}{2}$CD=9．
点评 本题考查了解直角三角形，掌握锐角三角函数的定义是解题的关键，属于基础题．
练习册系列答案
相关题目
12．估算$\sqrt{200}$的大小在哪两个数之间（ ）
| A． | 10到11之间 | B． | 14到15之间 | C． | 5到6之间 | D． | 20到21之间 |
13．二次函数y=x2-8x+1的最小值是（ ）
| A． | 4 | B． | -15 | C． | -4 | D． | 15 |
如图，已知线段AB=10cm，AB上有一点C，且CA：BC=BC：AB，求AC的长．
甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与时间x（时）之间的函数关系，请根据图象解答下列问题：
如图，直线AB、CD相交于点O，∠DOE=90°．