题目内容
12.用同样大小的乒乓球按如图所示的方式摆放,第一个图形要1个乒乓球,第二个图形要3个乒乓球,第3个图形要6个乒乓球,第4个图形要10个乒乓球,执照这样的规律摆下去,则第n个图形要$\frac{1}{2}$n(n+1)乒乓球.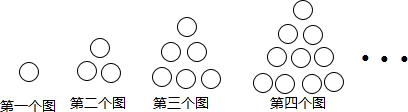
分析 根据已知图形中球的个数,发现第n个图形中球的数量为1+2+3+…+n,据此解答即可.
解答 解:∵第1个图形为1个小圆,即1=$\frac{1}{2}$×1×(1+1),
第2个图形为3个小圆,即3=$\frac{1}{2}$×2×(2+1),
第3个图形为6个小圆,即6=$\frac{1}{2}$×3×(3+1),
第4个图形为10个小圆,即10=$\frac{1}{2}$×4×(4+1),
…
∴第n个图形的小圆的个数为即$\frac{1}{2}$×n(n+1),
故答案为:$\frac{1}{2}$×n(n+1).
点评 此题考查了规律型:图形的变化类,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若一个角与它的余角相等,则这个角的度数为( )
| A. | 30° | B. | 35° | C. | 45° | D. | 60° |
17.下面的图形,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知点(2,3)在函数y=kx+1(k≠0)的图象上,那么下列各点中在此函数图象上的是( )
| A. | (-3,2) | B. | (3,4) | C. | (2,-3) | D. | (3,-2) |
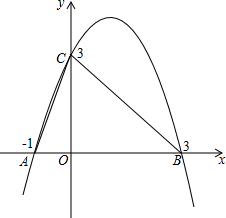 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3). 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是2$\sqrt{7}$-2.
如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是2$\sqrt{7}$-2.