题目内容
2.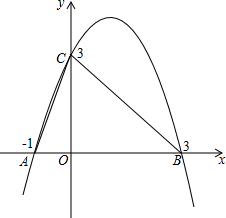 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).(1)求此抛物线的解析式;
(2)在直线BC上方的抛物线上是否存在一点M,使S△BCM最大,求出M的坐标;
(3)过抛物线的顶点D作过A,B,C三点的圆的切线,求此抛物线与x轴的交点的坐标.
分析 (1)设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可;
(2)过M点作MN∥y轴交BC于N,如图1,利用待定系数法求出直线BC的解析式为y=-x+3,设M(t,-t2+2t+3)(0<t<3),则N(t,-t+3),则可表示出MN=-t2+3t,利用三角形面积公式得到S△BMC=$\frac{1}{2}$MN•3=$\frac{3}{2}$(-t2+3t)=-$\frac{3}{2}$t2+$\frac{9}{2}$,然后根据二次函数的性质求解;
(3)先把(1)中解析式配成顶点式得到D(1,0),抛物线的对称轴为直线x=1,如图2,设直线x=1与x轴交于点G,则G(1,0),利用三角形外心的性质可确定△ABC的外接圆的圆心P的坐标为(1,1),则可计算出半径PB=$\sqrt{5}$,设切线DE、DF交x轴于E、F,如图2,作PH⊥DE于H,根据切线的性质得PH=PB=$\sqrt{5}$,然后证明Rt△DPH∽Rt△DEG,利用相似比求出GE,则可得到E点坐标,再利用点F与点E关于直线x=1对称确定F点坐标.
解答 解:(1)设抛物线解析式为y=a(x+1)(x-3),
把C(0,3)代入得a•1•(-3)=3,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-3),即y=-x2+2x+3;
(2)存在. 过M点作MN∥y轴交BC于N,如图1,
过M点作MN∥y轴交BC于N,如图1,
设直线BC的解析式为y=kx+b,把C(0,3),B(3,0)代入得$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
所以直线BC的解析式为y=-x+3,
设M(t,-t2+2t+3)(0<t<3),则N(t,-t+3),
所以MN=-t2+2t+3-(-t+3)=-t2+3t,
所以S△BMC=S△MNB+S△MNC=$\frac{1}{2}$MN•3=$\frac{3}{2}$(-t2+3t)=-$\frac{3}{2}$t2+$\frac{9}{2}$,
因为S△BMC=-$\frac{3}{2}$(t-$\frac{3}{2}$)2+$\frac{27}{8}$,
所以当t=$\frac{3}{2}$时,S△BMC取最大值$\frac{27}{8}$,此时M点的坐标为($\frac{3}{2}$,$\frac{15}{4}$);
(3) y=-x2+2x+3=-(x-1)2+4,则D(1,0),抛物线的对称轴为直线x=1,如图2,
y=-x2+2x+3=-(x-1)2+4,则D(1,0),抛物线的对称轴为直线x=1,如图2,
设直线x=1与x轴交于点G,则G(1,0),
△ABC的外接圆的圆心在直线x=1上,
因为△OBC为等边三角形,所以BC的垂直平分线为直线y=x,
当x=1时,y=1,则P点坐标为(1,1),PB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
切线DE、DF交x轴于E、F,如图2,作PH⊥DE于H,则PH=PB=$\sqrt{5}$,
在Rt△DPH中,PD=DG-PG=4-1=3,DH=$\sqrt{{3}^{2}-(\sqrt{5})^{2}}$=2,
因为∠PDH=∠EDG,
所以Rt△DPH∽Rt△DEG,
所以PH:GE=DH:DG,即$\sqrt{5}$:GE=2:4,解得GE=2$\sqrt{5}$,
所以E点坐标为(1+2$\sqrt{5}$,0),
因为点F与点E关于直线x=1对称,
所以F点坐标为(1-2$\sqrt{5}$,0),
即过点D的切线与x轴的交点坐标为(1-2$\sqrt{5}$)或(1+2$\sqrt{5}$,0).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和三角形外接圆的定义与切线的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用勾股定理和相似比求线段的长.

| A. | x2-1=y | B. | (x+2)(x+1)=x2 | C. | 6x2=0 | D. | x2=$\frac{1}{x}$ |
| A. | 1<x<3 | B. | 0<x<1 | C. | x<0,1<x<3 | D. | 0<x<1,x>3 |
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
 如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数直方图 |
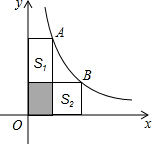 如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.
如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.