题目内容
2.如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)(1)填空:BC的长为4;
(2)求y关于x的函数关系式,并写出x的取值范围.

分析 (1)通过图2观察可知y=0时x=4,即D点从B运动到C平移的距离为4;
(2)当△DEF在平移过程中,与△ABC的重合部分有三种情况,将三种图形分别画出,通过作辅助线构造相似三角形,通过相似三角形对应边的关系,将各边用x表示出来,即可以列出y与x的函数关系式.
解答 解:(1)由图2得当x=4时,y=0,说明此时△DEF与△ABC无重合部分,
则点D从B到C运动的距离为4,即BC=4;
故答案为:4.
(2)当DE经过点A时(如图1),BD=3,CD=1,
∵△ABC≌△DEF.
∴∠EDF=∠BAC.
∵∠ACD=∠BCA
∴△ADC∽△BAC.
∴$\frac{AC}{BC}=\frac{DC}{AC}$,即$\frac{AC}{4}=\frac{1}{AC}$.AC=2
∴n=2
当0≤x≤2时(如图2),
设ED、EF与AB分别相交于点M,G,作MN⊥BC,垂足为N.
则∠MNB=90°=∠EFD=∠C.
∵∠MDN=∠EDF.
∴△DMN∽△DEF.
∴$\frac{MN}{EF}=\frac{DN}{DF}$,即$\frac{MN}{4}=\frac{DN}{2}$.
∴MN=2DN.
设DN=n,则MN=2n.
同理△BMN∽△BAC.
∴$\frac{MN}{AC}=\frac{BN}{BC}$.即$\frac{2n}{2}=\frac{BN}{4}$,
∴BN=4n,即x+n=4n.
∴n=$\frac{1}{3}$x.
∴S△BDM=$\frac{1}{2}$•BD•MN=$\frac{1}{2}•x•\frac{2}{3}x=\frac{1}{3}x$2
同理△BGF∽△BAC
∴$\frac{GF}{AC}=\frac{BF}{BC}$,即$\frac{GF}{2}=\frac{x+2}{4}$.
∴GF=$\frac{1}{2}(x+2)$,
∴y=S△BGF-S△BDM=$\frac{1}{2}(x+2)•\frac{1}{2}(x+2)-\frac{1}{3}x$2=-$\frac{1}{12}$x2+x+1.
当2<x≤3时(如图3),
由①知,S△BDM=$\frac{1}{3}$x2.
∴y=S△ABC-S△BDM=$\frac{1}{2}×2×4-\frac{1}{3}x$2=-$\frac{1}{3}$x2+4
当3<x≤4时(如图4),
设DE与AB相交于点H.
同理△DHC∽△DEF.
∴$\frac{HC}{EF}=\frac{DC}{DF}$,即$\frac{HC}{4}=\frac{4-x}{2}$
∴HC=24-x.
∴y=$\frac{1}{2}•DC•HC=\frac{1}{2}(4-x)•2(4-x)$=x2-8x+16
∴y=$\left\{\begin{array}{l}{-\frac{1}{12}x^2+x+1(0≤x≤2)}\\{-\frac{1}{3}x^2+4(2<x≤3)}\\{x^2-8x+16(3<x≤4)}\end{array}\right.$.
点评 本题考查了平移的性质、相似三角形性质,解题的关键是要找到△DEF运动过程中与△ABC重叠面积的不同情况,通过辅助线构造相似三角形,要注意分类讨论画出对应的图象.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | 抛出的篮球会下落 | |
| B. | 打开电视,正在播《最强大脑》 | |
| C. | 任意买一张电影票,座位号是2的倍数 | |
| D. | 你最喜欢的篮球队将夺得CBA冠军 |
 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为16,则AC与BD的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为16,则AC与BD的和是( )| A. | 10 | B. | 16 | C. | 20 | D. | 22 |
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{30}$ |
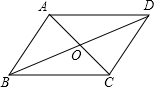 如图,平行四边形ABCD的对角线相交于点O,BC=7,BD=10,AC=6,则△AOD的周长是15.
如图,平行四边形ABCD的对角线相交于点O,BC=7,BD=10,AC=6,则△AOD的周长是15. 如图,BC⊥AE于点C,AB∥CD,∠B=48°,则∠ECD=42°.
如图,BC⊥AE于点C,AB∥CD,∠B=48°,则∠ECD=42°.