题目内容
3.计算(1)(2$\sqrt{48}$-3$\sqrt{27}$)÷$\sqrt{6}$
(2)2$\sqrt{12}$+3$\sqrt{1\frac{1}{3}}$-$\sqrt{5\frac{1}{3}}$-$\frac{2}{3}$$\sqrt{48}$
(3)已知x=$\frac{2}{1+\sqrt{3}}$,y=$\frac{2}{1-\sqrt{3}}$,求x2+y2.
分析 (1)先把括号内的各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)先利用分母有理化化简x和y,再计算x+y与xy的值,然后利用完全平方公式把原式变形为(x+y)2-2xy,再利用整体代入的方法计算.
解答 解:(1)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{1}{\sqrt{2}}$
=-$\frac{\sqrt{2}}{2}$;
(2)原式=4$\sqrt{3}$+2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{8\sqrt{3}}{3}$
=2$\sqrt{3}$;
(3)x=$\sqrt{3}$-1,y=-($\sqrt{3}$+1)=-$\sqrt{3}$-1,
所以x+y=-2,xy=-2,
所以原式=(x+y)2-2xy
=(-2)2-2×(-2)
=8.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14. 如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
 如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
11.要反映2015年末嘉兴市各个县(区)常住人口占嘉兴市总人口的比例,宜采用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数直方图 |
8.下列各值中是方程组$\left\{\begin{array}{l}a+b=3\\ a-b=1\end{array}$的解的是( )
| A. | $\left\{\begin{array}{l}a=1\\ b=2\end{array}$ | B. | $\left\{\begin{array}{l}a=2\\ b=1\end{array}$ | C. | $\left\{\begin{array}{l}a=3\\ b=1\end{array}$ | D. | $\left\{\begin{array}{l}a=4\\ b=5\end{array}$ |
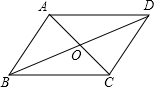 如图,平行四边形ABCD的对角线相交于点O,BC=7,BD=10,AC=6,则△AOD的周长是15.
如图,平行四边形ABCD的对角线相交于点O,BC=7,BD=10,AC=6,则△AOD的周长是15.