��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬B����ԭ����Ҳ࣬A�������Ϊ��-1��0������y�ύ��C��0��-3������P��ֱ��BC�·�����������һ���㣮
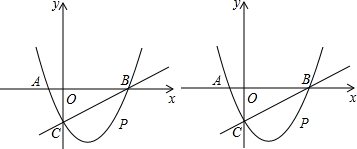
��1����������κ����ı���ʽ��
��2������P�˶���ʲôλ��ʱ���ı���ABPCΪ�������Σ�ֱ��д����ʱP������ꣻ
��3������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��4������P�˶���ʲôλ��ʱ����BPC�������������ʱP������꣮

��1����������κ����ı���ʽ��
��2������P�˶���ʲôλ��ʱ���ı���ABPCΪ�������Σ�ֱ��д����ʱP������ꣻ
��3������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��4������P�˶���ʲôλ��ʱ����BPC�������������ʱP������꣮
���㣺���κ����ۺ���
ר�⣺
��������1��ֱ�Ӱ�A��-1��0����C��0��-3������y=x2+bx+c�ɵõ�����b��c�ķ����飬�ⷽ�������b=-2��c=-3������κ����ı���ʽΪy=x2-2x-3��
��2������������Ϊ��Գ�ͼ�Σ�Ҫ�õ��ı���ABPCΪ�������Σ�ֻ��PC��AB�����P���C���������ϵĶԳƵ㣬����������ߵĶԳ���Ϊֱ��x=1�����ǿɵõ���C��0��-3������ֱ��x=1�ԳƵĵ�P������Ϊ��2��-3����
��3����OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P����PO=PC�����ݷ��۵����ʵ�OP��=OP��CP��=CP�����ı���POP��CΪ���Σ���E������Ϊ��0��-
�������P��������Ϊ-
���ٰ�y=
����y=x2-2x-3�������Ӧx��ֵ��Ȼ��ȷ������������P�����꣮
��4����P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ������á�BPC��������ɴ˿ɵõ����ڡ�BPC�������P�������ĺ�����ϵʽ�����ݺ��������ʼ��������BPC��������ʱ��Ӧ��P������꣮
��2������������Ϊ��Գ�ͼ�Σ�Ҫ�õ��ı���ABPCΪ�������Σ�ֻ��PC��AB�����P���C���������ϵĶԳƵ㣬����������ߵĶԳ���Ϊֱ��x=1�����ǿɵõ���C��0��-3������ֱ��x=1�ԳƵĵ�P������Ϊ��2��-3����
��3����OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P����PO=PC�����ݷ��۵����ʵ�OP��=OP��CP��=CP�����ı���POP��CΪ���Σ���E������Ϊ��0��-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
��4����P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ������á�BPC��������ɴ˿ɵõ����ڡ�BPC�������P�������ĺ�����ϵʽ�����ݺ��������ʼ��������BPC��������ʱ��Ӧ��P������꣮
����⣺��1����A��-1��0����C��0��-3������y=x2+bx+c��
��
 ���
���
��
��������κ����ı���ʽΪy=x2-2x-3��
��2����ͼ1���ߵ�P��ֱ��BC�·�����������һ���㣬�ı���ABPCΪ�������Σ�
��PC��AB��
���P���C���������ϵĶԳƵ㣬
�������ߵĶԳ���Ϊֱ��x=-
=1��
���C��0��-3������ֱ��x=1�ԳƵĵ�P������Ϊ��2��-3����
��3�����ڣ��������£�
 ��OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P������Ϊ��E����ͼ2��
��OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P������Ϊ��E����ͼ2��
��PO=PC��
�ߡ�POC��CO���ۣ��õ��ı���POP��C��
��OP��=OP��CP��=CP��
��OP��=OP=CP��=CP��
���ı���POP��CΪ���Σ�
��C��������0��-3����
��E��������0��-
����
���P��������Ϊ-
��
��y=-
����y=x2-2x-3��x2-2x-3=-
��
���x=
��
�ߵ�P��ֱ��BC�·����������ϣ�
��x=
��
�����������ĵ�P������Ϊ��
��-
����
 ��4����ͼ3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x��x2-2x-3����
��4����ͼ3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x��x2-2x-3����
�ã�ֱ��BC�Ľ���ʽΪy=x-3
��Q���������x��x-3����
S��BPC=S��BPQ+S��CPQ
=
QP•BF+
QP•OF
=
��-x2+3x����3
=-
��x-
��2+
��
��x=
ʱ����BPC��������
��ʱP�������Ϊ��
��-
����
|
 ���
���
|
��������κ����ı���ʽΪy=x2-2x-3��
��2����ͼ1���ߵ�P��ֱ��BC�·�����������һ���㣬�ı���ABPCΪ�������Σ�
��PC��AB��
���P���C���������ϵĶԳƵ㣬
�������ߵĶԳ���Ϊֱ��x=-
| -2 |
| 2��1 |
���C��0��-3������ֱ��x=1�ԳƵĵ�P������Ϊ��2��-3����
��3�����ڣ��������£�
 ��OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P������Ϊ��E����ͼ2��
��OC�Ĵ�ֱƽ���߽�ֱ��BC�·����������ڵ�P������Ϊ��E����ͼ2����PO=PC��
�ߡ�POC��CO���ۣ��õ��ı���POP��C��
��OP��=OP��CP��=CP��
��OP��=OP=CP��=CP��
���ı���POP��CΪ���Σ�
��C��������0��-3����
��E��������0��-
| 3 |
| 2 |
���P��������Ϊ-
| 3 |
| 2 |
��y=-
| 3 |
| 2 |
| 3 |
| 2 |
���x=
2��
| ||
| 2 |
�ߵ�P��ֱ��BC�·����������ϣ�
��x=
2+
| ||
| 2 |
�����������ĵ�P������Ϊ��
2+
| ||
| 2 |
| 3 |
| 2 |
 ��4����ͼ3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x��x2-2x-3����
��4����ͼ3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x��x2-2x-3�����ã�ֱ��BC�Ľ���ʽΪy=x-3
��Q���������x��x-3����
S��BPC=S��BPQ+S��CPQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
��x=
| 3 |
| 2 |
��ʱP�������Ϊ��
| 3 |
| 2 |
| 15 |
| 4 |
���������⿼���˶��κ����ۺ��⣺���κ���y=ax2+bx+c��a��b��cΪ������a��0����ͼ��Ϊ�����ߣ��䶥��ʽΪy=a��x-
��2+
�������ߵĶԳ���Ϊx=-
����a��0��y��Сֵ=
����a��0��y���ֵ=
���������ϵĵ�ĺ����������������ߵĽ���ʽ�����������ı��ε��ж��������Լ����ɶ���Ҫ�������ã�ͬʱ������ͼ���������֪ʶ�㣮
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 4ac-b2 |
| 4a |

��ϰ��ϵ�д�
�����Ŀ
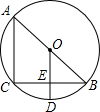 ��ͼ��AB�ǡ�O��ֱ����BC���ң�OD��BC������ΪE������O��D������AC��
��ͼ��AB�ǡ�O��ֱ����BC���ң�OD��BC������ΪE������O��D������AC��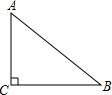 ��ͼ����֪Rt��ABC�У���C=90�㣬AC=3��BC=4����AB�ij��͡�ABC���ܳ���
��ͼ����֪Rt��ABC�У���C=90�㣬AC=3��BC=4����AB�ij��͡�ABC���ܳ���