题目内容
4.下列几组数据中,能作为直角三角形三边长的是( )| A. | 2,3,4 | B. | 1,2,3 | C. | 1,$\frac{1}{2}$,$\frac{1}{3}$ | D. | 7,24,25 |
分析 根据勾股定理的逆定理对各选项进行逐一判断即可.
解答 解:A、∵22+32=13≠42,∴不能构成直角三角形,故本选项错误;
B、∵12+22=5≠32,∴不能构成直角三角形,故本选项错误;
C、∵($\frac{1}{2}$)2+($\frac{1}{3}$)2=$\frac{13}{36}$≠12,∴不能构成直角三角形,故本选项错误;
D、∵72+242=625=252,∴能构成直角三角形,故本选项正确.
故选D.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
14.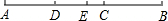 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
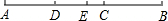 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A. | 8cm | B. | 12cm | C. | 14cm | D. | 10cm |
15.若方程x2-3x-1=0的两根为x1、x2,则x1x2的值为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
12.如果xy3m与-5xny9是同类项,则m、n的值分别为( )
| A. | 3,1 | B. | 1,3 | C. | 3,0 | D. | 0,2 |
19.已知点A的坐标为(-3,5),那么点A关于x轴和y轴对称的点的坐标分别为( )
| A. | (-3,-5)(3,5) | B. | (-3,5)(3,-5) | C. | (3,5)(-3,-5) | D. | (3,-5)(-3,5) |
16.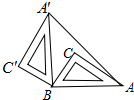 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
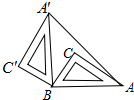 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
14.若|a|=8,则a的值是( )
| A. | -8 | B. | 8 | C. | ±8 | D. | ±$\frac{1}{8}$ |