题目内容
3.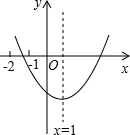 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②⑤ | D. | ③④⑤ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答 解:①根据图示知,二次函数与x轴有两个交点,所以△=b2-4ac>0,即b2>4ac;故本选项正确;
②∵对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a,
∴2a+b=0;故本选项正确;
③由函数的图象知:当x=-1时,y<0;即a-b+c<0,
∵b=-2a,
∴a+2a+c<0,即3a+c<0,故本选项错误;
④由函数的图象知:当x=-2时,y>0;即4a-2b+c>0,故本选项错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故本选项正确;
所以结论正确的是①②⑤.
故选C.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
11. 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
18.下列命题中,属于真命题的是( )
| A. | 各边相等的多边形是正多边形 | B. | 同角或等角的余角相等 | ||
| C. | 必然事件发生的概率为0 | D. | 六边形的内角和等于540° |
8.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | $\sqrt{8}$ | D. | 3 |
12.给出下列5个命题:①相等的角是对顶角;②互补的两个角中一定是一个为锐角,另一个为钝角;③平行于同一条直线的两条直线平行;④同旁内角的平分线互相垂直.其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.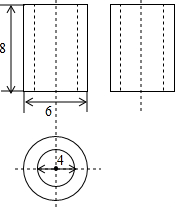 如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )
如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )
 如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )
如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )| A. | 9π | B. | 40π | C. | 20π | D. | 16π |
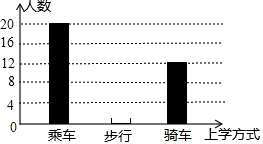 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.
学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.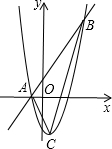 如图,抛物线y=a(x-1)2-n与直线y=2x+b相交于点A(-1,0)和点B(m,12).
如图,抛物线y=a(x-1)2-n与直线y=2x+b相交于点A(-1,0)和点B(m,12).