题目内容
2.计算(1)($\frac{1}{2}$)-1+(2-π)0+(-3)4÷(-3)2
(2)(-a2)3+(-a3)2-a2•a3
(3)(a-b)10÷(b-a)4•(a-b)3
(4)3a2(a3b2-2a)-4a(-a2b)2.
分析 (1)先计算负整数指数幂,零指数幂,乘方,再算除法,再计算加减法即可求解;
(2)先算积的乘方,同底数幂的乘除法,再合并同类项即可求解;
(3)根据同底数幂的乘除法的计算法则计算即可求解;
(4)先算单项式乘以多项式,积的乘方,再算单项式乘以单项式,再合并同类项即可求解.
解答 解:(1)($\frac{1}{2}$)-1+(2-π)0+(-3)4÷(-3)2
=2+1+81÷9
=2+1+9
=12;
(2)(-a2)3+(-a3)2-a2•a3
=-a6+a6-a6
=-a6;
(3)(a-b)10÷(b-a)4•(a-b)3
=(a-b)10-4+3
=(a-b)9;
(4)3a2(a3b2-2a)-4a(-a2b)2.
=3a5b2-6a3-4a•a4b2
=3a5b2-6a3-4a5b2
=-a5b2-6a3.
点评 考查了整式的混合运算,注意:(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.同时考查了实数的运算.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.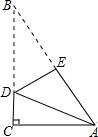 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
14.一个六边形,每一个内角都相等,每个内角的度数为( )
| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
11.下列命题中,逆命题成立的是( )
| A. | 两个全等三角形的对应角相等 | |
| B. | 如果两个实数是正数,那么它们的积是正数 | |
| C. | 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形 | |
| D. | 如果两个角是直角,那么它们相等 |
 在如图所示的5×5方格纸中,点A、B在边长为1小正方形的格点上,点C也在正方形的格点上.已知△ABC面积为2,在图中的方格纸中,满足条件的C点有5个.
在如图所示的5×5方格纸中,点A、B在边长为1小正方形的格点上,点C也在正方形的格点上.已知△ABC面积为2,在图中的方格纸中,满足条件的C点有5个.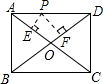 如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.
如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.