题目内容
10.用同样大小的黑色棋子按如图所示的方式摆放图形,按照这样的规律摆下去,则第11个图形需棋子颗数为( )
| A. | 28 | B. | 31 | C. | 34 | D. | 37 |
分析 解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
解答 解:∵第一个图需棋子3+1=4;
第二个图需棋子3×2+1=7;
第三个图需棋子3×3+1=10;
…
∴第11个图需棋子3×11+1=34枚.
故选:C.
点评 本题考查了规律型:图形的变化类:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
相关题目
20.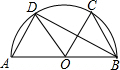 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
15.十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面树(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
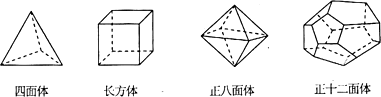
(1)根据上面多面体模型,填写表格中的空格:
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2(用所给的字母表达);
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.

(1)根据上面多面体模型,填写表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
2.下列命题中,假命题的是( )
| A. | 同旁内角相等,两直线平行 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 同角(等角)的补角相等 | |
| D. | 三角形的一个外角大于任何一个与它不相邻的内角 |
 如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.
如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.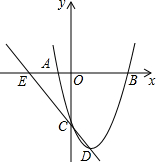 如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,-3).