题目内容
7.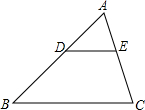 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.
分析 先根据平行线分线段成比例得到$\frac{AD}{BD}$=$\frac{AE}{EC}$,则可计算出EC,然后计算AE+EC即可.
解答 解:∵DE∥BC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$,即$\frac{4}{6}$=$\frac{3}{EC}$,
∴EC=$\frac{9}{2}$,
∴AC=AE+EC=3+$\frac{9}{2}$=$\frac{15}{2}$.
故答案为$\frac{15}{2}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
17.已知多项式2x2y|m|-1-$\frac{1}{4}$(m+2)y2+5是关于x、y的三次二项式,则m等于( )
| A. | ±2 | B. | 2 | C. | -2 | D. | -1 |
 如图,在△ABC中,∠B=30°,∠C=45°,AB=8,求AC、BC的长度(结果保留根号).
如图,在△ABC中,∠B=30°,∠C=45°,AB=8,求AC、BC的长度(结果保留根号).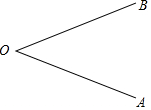 如图,∠AOB
如图,∠AOB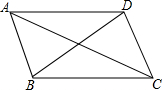 如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )
如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )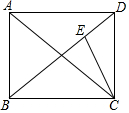 如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.
如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.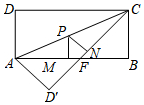 如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.