题目内容
请阅读材料:规定a⊕b=
-
,例如:3⊕2=
-
=-
.按照这种运算规定,请你解答下列各题:
(1)求4⊕3的值;
(2)若x⊕1=1,请求出x的值.
| a |
| a+b |
| 1 |
| a-b |
| 3 |
| 3+2 |
| 1 |
| 3-2 |
| 2 |
| 5 |
(1)求4⊕3的值;
(2)若x⊕1=1,请求出x的值.
考点:解分式方程,有理数的混合运算
专题:新定义
分析:(1)根据题中的新定义化简所求式子,计算即可得到结果;
(2)利用题中的新定义化简已知等式,求出方程的解即可得到x的值.
(2)利用题中的新定义化简已知等式,求出方程的解即可得到x的值.
解答:解:(1)4⊕3=
-
=-
;
(2)∵x⊕1=1由题意得
-
=1,
去分母得:x(x-1)-(x+1)=x2-1,
去括号得:x2-x-x-1=x2-1,
移项合并得:-2x=0,
解得:x=0,
经检验:x=0是原方程的解,
则x⊕1=1时,x=0.
| 4 |
| 4+3 |
| 1 |
| 4-3 |
| 3 |
| 7 |
(2)∵x⊕1=1由题意得
| x |
| x+1 |
| 1 |
| x-1 |
去分母得:x(x-1)-(x+1)=x2-1,
去括号得:x2-x-x-1=x2-1,
移项合并得:-2x=0,
解得:x=0,
经检验:x=0是原方程的解,
则x⊕1=1时,x=0.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
 如图,已知直线EF与AB、CD分别相交于点G、H,且∠1=∠3,那么AB与CD平行吗?为什么?
如图,已知直线EF与AB、CD分别相交于点G、H,且∠1=∠3,那么AB与CD平行吗?为什么?
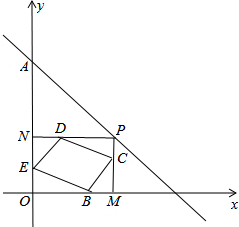 如图,已知一次函数y=-
如图,已知一次函数y=- 如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).