题目内容
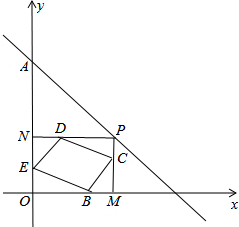 如图,已知一次函数y=-
如图,已知一次函数y=-| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(1)b=
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=-
| 1 |
| 2 |
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得b的值;
(2)根据矩形的判定与性质,可得PM与ON,PN与OM的关系,根据PC=
MP,MB=
OM,OE=
ON,NO=
NP,可得PC与OE,CM与NE,BM与ND,OB与PD的关系,根据全等三角形的判定与性质,可得BE与CD,BC与DE的关系,根据平行四边形的判定,可得答案;
(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
(2)根据矩形的判定与性质,可得PM与ON,PN与OM的关系,根据PC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
解答:解:(1)一次函数y=-
x+b的图象过点A(0,3),
3=-
×0+b,
解得b=3.
故答案为:3;
(2)证明:过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=
MP,MB=
OM,OE=
ON,NO=
NP,
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,
,
∴△OBE≌△PDC(SAS),
BE=DC.
在△MBC和△NDE中,
,
∴△MBC≌△NDE(SAS),
DE=BC.
∵BE=DC,DE=BC,
∴四边形BCDE是平行四边形;
(3)设P点坐标(x,y),
当△OBE≌△MCB时,四边形BCDE为正方形,
OE=BM,
即
y=
x,
x=y.
P点在直线上,
,
解得
在直线y=-
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2).
| 1 |
| 2 |
3=-
| 1 |
| 2 |
解得b=3.
故答案为:3;
(2)证明:过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,
|
∴△OBE≌△PDC(SAS),
BE=DC.
在△MBC和△NDE中,
|
∴△MBC≌△NDE(SAS),
DE=BC.
∵BE=DC,DE=BC,
∴四边形BCDE是平行四边形;
(3)设P点坐标(x,y),
当△OBE≌△MCB时,四边形BCDE为正方形,
OE=BM,
即
| 1 |
| 3 |
| 1 |
| 3 |
x=y.
P点在直线上,
|
解得
|
在直线y=-
| 1 |
| 2 |
点评:本题考查了一次函数的综合题,利用了全等三角形的判定与性质,平行四边形的判定与性质,正方形的性质.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
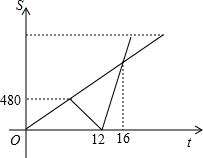 如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.
如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.