题目内容
 如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).(1)当k=1时,求一次函数的解析式,并直接在坐标系中画出直线l;
(2)通过计算说明:点C在直线l上;
(3)若线段AB与直线l有交点,求k的取值范围.
考点:一次函数的性质,一次函数的图象,一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:
分析:(1)直接将k=1代入求出即可;
(2)将C点代入函数解析式进而判断得出即可;
(3)分别利用当直线y=kx+4-3k过B(1,2)时,k值最小,当直线y=kx+4-3k过A(2,0)时,k值最大,求出即可.
(2)将C点代入函数解析式进而判断得出即可;
(3)分别利用当直线y=kx+4-3k过B(1,2)时,k值最小,当直线y=kx+4-3k过A(2,0)时,k值最大,求出即可.
解答: 解:(1)把k=1代入y=kx+4-3k中得:y=x+1;
解:(1)把k=1代入y=kx+4-3k中得:y=x+1;
(2)把C(3,4)代入y=x+1中:4=3+1,
因此C在直线l上;
(3)当直线y=kx+4-3k过B(1,2)时,k值最小,则k+4-3k=2,解得k=1;
当直线y=kx+4-3k过A(2,0)时,k值最大,则2k+4-3k=0,解得k=4,
故k的取值范围为1≤k≤4.
 解:(1)把k=1代入y=kx+4-3k中得:y=x+1;
解:(1)把k=1代入y=kx+4-3k中得:y=x+1;(2)把C(3,4)代入y=x+1中:4=3+1,
因此C在直线l上;
(3)当直线y=kx+4-3k过B(1,2)时,k值最小,则k+4-3k=2,解得k=1;
当直线y=kx+4-3k过A(2,0)时,k值最大,则2k+4-3k=0,解得k=4,
故k的取值范围为1≤k≤4.
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
 如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证:
如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证: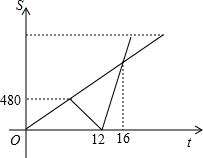 如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.
如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.