题目内容
11.观察下列一列数,探求其规律:-1,$\frac{1}{2}$,-$\frac{1}{3}$,$\frac{1}{4}$,-$\frac{1}{5}$,$\frac{1}{6}$,…第n个数是$\frac{(-1)^{n}}{n}$.
分析 观察已知,发现该列数,奇数项为负数,偶数项为正数,分数的分子为1,分母为等差数列,由此求出答案.
解答 解:观察已知一列数,
第1个数:-1=(-1)1×$\frac{1}{1}$,
第2个数:-1=(-1)2×$\frac{1}{2}$,
第3个数:-1=(-1)3×$\frac{1}{3}$,
第4个数:-1=(-1)4×$\frac{1}{4}$,
第5个数:-1=(-1)5×$\frac{1}{5}$,
第6个数:-1=(-1)6×$\frac{1}{6}$,
…
第n个数:(-1)n×$\frac{1}{n}$=$\frac{(-1)^{n}}{n}$.
故答案为:$\frac{(-1)^{n}}{n}$.
点评 题目考查了数字的变化规律,解决此类问题的关键是找出所求数字与序号的关系,题目整体较为简单,适合随堂训练.

练习册系列答案
相关题目
2. 如图,Rt△ABC中,∠C=90°,CD⊥AB于D,E是AC的中点,则下列结论中一定正确的是( )
如图,Rt△ABC中,∠C=90°,CD⊥AB于D,E是AC的中点,则下列结论中一定正确的是( )
 如图,Rt△ABC中,∠C=90°,CD⊥AB于D,E是AC的中点,则下列结论中一定正确的是( )
如图,Rt△ABC中,∠C=90°,CD⊥AB于D,E是AC的中点,则下列结论中一定正确的是( )| A. | ∠4=∠5 | B. | ∠1=∠2 | C. | ∠4=∠3 | D. | ∠B=∠2 |
20.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工王师傅2013年月退休金为1800元,2015年达到2460元.设王师傅的月退休金从2013年到2015年年平均增长率为x,可列方程为( )
| A. | 2460(1-x)2=1800 | B. | 1800(1+x)2=2460 | ||
| C. | 1800(1-x)2=2460 | D. | 1800+1800(1+x)+1800(1+x)2=2460 |
 如图,从点O引出6条射线OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度数.
如图,从点O引出6条射线OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度数.

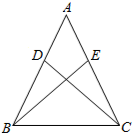 已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.
已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.