题目内容
7.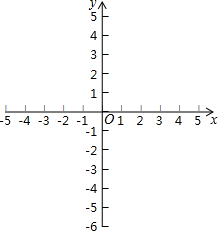 已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.
已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.(1)求OT所在直线的解析式;
(2)求直线l和直线OT与x轴所围成的图形的面积.
分析 (1)由点T在直线l上,将点T坐标代入直线l解析式求得T的坐标,再用待定系数法可求直线OT解析式;
(2)求出直线l与x轴交点,根据三角形面积公式计算即可.
解答 解:(1)根据题意,将点T(t,$\frac{2}{3}$)代入y=-2x+2,
得:-2t+2=$\frac{2}{3}$,
解得:t=$\frac{2}{3}$,
∴点T($\frac{2}{3}$,$\frac{2}{3}$),
设OT所在直线的解析式为:y=kx,
将点T($\frac{2}{3}$,$\frac{2}{3}$)代入,解得:k=1,
故OT所在直线的解析式为:y=x;
(2)在直线l:y=-2x+2中,当y=0时x=1,
故直线l与x轴交与点(1,0),
∴直线l和直线OT与x轴所围成的图形的面积为:$\frac{1}{2}$×$\frac{2}{3}$×1=$\frac{1}{3}$.
点评 本题主要考查待定系数法求一次函数解析式和三角形面积计算,熟练掌握待定系数法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.如果∠2是∠1的余角,∠3是∠1的补角,那么∠2和∠3的关系是( )
| A. | ∠3-∠2=90° | B. | ∠3+∠2=90° | C. | ∠3=∠2 | D. | 没有关系 |
12. 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
16.如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2,那么tanα=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
 Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.
Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.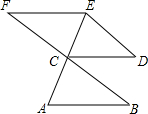 如图,点C既是AE的中点,也是BF为中点,AB∥CD,∠D=∠F,说明BC∥DE的理由.
如图,点C既是AE的中点,也是BF为中点,AB∥CD,∠D=∠F,说明BC∥DE的理由.