题目内容
9. 如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.
如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.
分析 先根据角平分线的定义得出∠CAE=∠BAE,再由平行线的性质得出∠CAE=∠AED,故可得出∠AED=∠BAE,即AD=DE,再由点D是线段AB的中点可知AD=DE=$\frac{1}{2}$AB,由此可得出结论.
解答 解:∵AP平分∠BAC,
∴∠CAE=∠BAE.
∵DE∥AC,
∴∠CAE=∠AED,
∴∠AED=∠BAE,即AD=DE.
∵点D是线段AB的中点,
∴AD=DE=$\frac{1}{2}$AB,
∴∠AEB=90°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
 如图,已知∠1=∠2,∠B=30°,则∠3=30°.
如图,已知∠1=∠2,∠B=30°,则∠3=30°.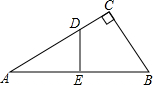 如图,在Rt△ABC中,∠C=90°,∠A=30°,DE垂直平分AB.若AD=6,则CD的长等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,DE垂直平分AB.若AD=6,则CD的长等于( )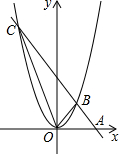 如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点的坐标为(1,1).
如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点的坐标为(1,1).