题目内容
1.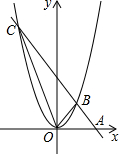 如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点的坐标为(1,1).
如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点的坐标为(1,1).(1)求直线AB的表达式及抛物线y=ax2的表达式;
(2)求点C的坐标;
(3)求S△COB;
(4)若抛物线上有一点D(在第一象限内),使得S△AOD=S△COB,求点D的坐标.
分析 (1)利用待定系数法求直线AB的解析式为y=-x+2;然后把B(1,1)代入y=ax2得a=1,从而得到抛物线解析式;
(2)通过解方程组$\left\{\begin{array}{l}{y=-x+2}\\{y={x}^{2}}\end{array}\right.$可得C点坐标;
(3)根据三角形面积公式,利用S△COB=S△COA-S△AOB进行计算;
(4)根据二次函数图象上点的坐标特征,可设D(t,t2)(t>0),利用三角形面积公式得到$\frac{1}{2}$•2•t2=3,然后解出t的值即可得到D点坐标.
解答 解:(1)设直线AB的解析式为y=kx+b,
把A(2,0),B(1,1)代入得$\left\{\begin{array}{l}{2k+b=0}\\{k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
所以直线AB的解析式为y=-x+2;
把B(1,1)代入y=ax2得a=1,
所以抛物线解析式为y=x2;
(2)解方程组$\left\{\begin{array}{l}{y=-x+2}\\{y={x}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$,
所以C(-2,4);
(3)S△COB=S△COA-S△AOB=$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×1=3;
(4)设D(t,t2)(t>0),
∵S△AOD=S△COB,
∴$\frac{1}{2}$•2•t2=3,解得t=$\sqrt{3}$或t=-$\sqrt{3}$(舍去),
∴D($\sqrt{3}$,3).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了待定系数法求一次函数解析式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{1}{12x}$ | D. | y=-$\frac{1}{12x}$ |
| 全月应纳税金额 | 税率(%) |
| 不超过1500元 | 3% |
| 超过1500元至4500元的部分 | 10% |
| 超过4500元至9000元的部分 | 20% |
| … | … |
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为x元(5000<x<8000),应交的个人所得税为y元,求y与x之间的函数关系式;
(3)若王教授的月工资不超过10000元,他每月的纳税金额超过月工资的$\frac{1}{15}$吗?若能,请给出王教授的工资范围;若不能,请说明理由.
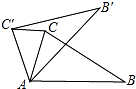 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠CAC′为( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠CAC′为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )| A. | 22cm | B. | 20cm | C. | 18cm | D. | 16cm |
 如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.
如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.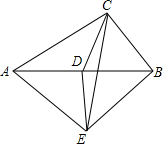 已知在Rt△ABC中,AC>BC,∠ACB=90°,点D是AB边的中点,过点D作DE⊥AB于点D,交∠ACB的角平分线于点E,连接AE,BE.证明:AE=EB,并且AE⊥EB.
已知在Rt△ABC中,AC>BC,∠ACB=90°,点D是AB边的中点,过点D作DE⊥AB于点D,交∠ACB的角平分线于点E,连接AE,BE.证明:AE=EB,并且AE⊥EB.