题目内容
4.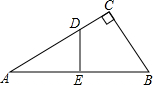 如图,在Rt△ABC中,∠C=90°,∠A=30°,DE垂直平分AB.若AD=6,则CD的长等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,DE垂直平分AB.若AD=6,则CD的长等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据线段的垂直平分线的性质得到BD=AD=6,∠DBA=∠A=30°,根据直角三角形的性质求出CD的长.
解答  解:连接BD,
解:连接BD,
∵DE垂直平分AB,AD=6,
∴BD=AD=6,∠DBA=∠A=30°,
∵∠C=90°,∠A=30°,
∴∠CBA=60°,
∴∠CBD=30°,
∴CD=$\frac{1}{2}$BD=3,
故选:B.
点评 本题考查线段的垂直平分线的性质和直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15. 如图,点A、B、C在⊙O上,若∠C=40°,则∠AOB的度数为( )
如图,点A、B、C在⊙O上,若∠C=40°,则∠AOB的度数为( )
 如图,点A、B、C在⊙O上,若∠C=40°,则∠AOB的度数为( )
如图,点A、B、C在⊙O上,若∠C=40°,则∠AOB的度数为( )| A. | 20° | B. | 100° | C. | 80° | D. | 40° |
12.已知点A是反比例函数图象上一点,它到原点的距离为5,到x轴的距离为3,若点A在第二象限内,则这个反比例函数的表达式为( )
| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{1}{12x}$ | D. | y=-$\frac{1}{12x}$ |
16.《中华人民共和国个人所得税法》中规定,公民月工薪所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.即全月应纳税所得额=当月工资-3500元.个人所得税款按下表累进计算.
(例如:某人月工资为5500元,需交个人所得税为(5500-3500-1500)×10%+1500×3%=95元)
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为x元(5000<x<8000),应交的个人所得税为y元,求y与x之间的函数关系式;
(3)若王教授的月工资不超过10000元,他每月的纳税金额超过月工资的$\frac{1}{15}$吗?若能,请给出王教授的工资范围;若不能,请说明理由.
| 全月应纳税金额 | 税率(%) |
| 不超过1500元 | 3% |
| 超过1500元至4500元的部分 | 10% |
| 超过4500元至9000元的部分 | 20% |
| … | … |
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为x元(5000<x<8000),应交的个人所得税为y元,求y与x之间的函数关系式;
(3)若王教授的月工资不超过10000元,他每月的纳税金额超过月工资的$\frac{1}{15}$吗?若能,请给出王教授的工资范围;若不能,请说明理由.
13. 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )| A. | 22cm | B. | 20cm | C. | 18cm | D. | 16cm |
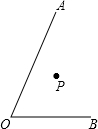 如图,已知∠AOB及∠AOB内部的一点P.
如图,已知∠AOB及∠AOB内部的一点P. 如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.
如图,点D是线段AB的中点,AP平分∠BAC,DE∥AC,交AP于E,连接BE,请运用所学知识,确定∠AEB的度数.