题目内容
4．
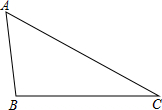如图，在△ABC中，AB=3，BC=5，AC=6，请解答下列问题：（1）尺规作图：将△ABC补成一个?ABCD．（要求：不写作法，保留作图痕迹）
（2）求（1）中?ABCD的面积．
分析 （1）先作AC的垂直平分线得到AC的中点O，再延长BO到点D，使OD=OB，则四边形ABCD为平行四边形；
（2）作AH⊥BC于H，如图，利用勾股定理得到AH2=32-BH2，AH2=62-（5+BH）2，则可求出BH和AH，然后根据平行四边形的面积公式求解．
解答 解：（1）如图，平行四边形ABCD为所作；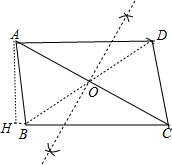
（2）作AH⊥BC于H，如图，
在Rt△ABH中，AH2=AB2-BH2=32-BH2，
在Rt△ACH中，AH2=AC2-CH2=62-（5+BH）2，
则32-BH2=62-（5+BH）2，解得BH=$\frac{1}{5}$，
所以AH=$\sqrt{{3}^{2}-（\frac{1}{5}）^{2}}$=$\frac{4\sqrt{14}}{5}$，
所以?ABCD的面积=$\frac{4\sqrt{14}}{5}$×5=4$\sqrt{14}$．
点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行四边形的性质．
练习册系列答案
相关题目
14．下列各式中最简二次根式为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{{x}^{2}}$ | C． | $\sqrt{0.7}$ | D． | $\sqrt{\frac{1}{3}}$ |
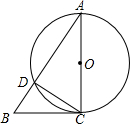如图，AC是⊙O的直径，∠A=30°，AB交⊙O于D，CD=1，
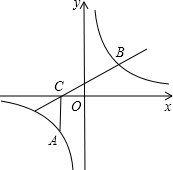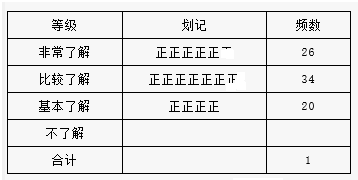
如图，点A为双曲线y=$\frac{k}{x}$（k＞0）上一点，AC⊥x轴于C，过C的直线l交双曲线于B，∠BCO=30°，BC=2$\sqrt{3}$，点A横坐标为-1．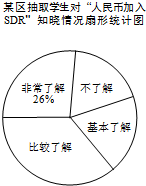
“世界那么大，我想去看看”一句话红遍网络，随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR（特别提款权），以后出国看世界更加方便．为了解某区6000名初中生对“人民币加入SDR”知晓的情况，某校数学兴趣小组随机抽取区内部分初中生进行问卷调查，将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级，并将调查结果整理分析，得到下列图表：
13．下列二次根式中属于最简二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{\frac{a}{b}}$ | C． | $\sqrt{{a}^{2}+1}$ | D． | $\sqrt{4a+4}$ |