题目内容
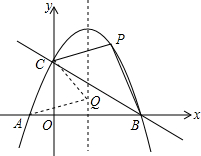 如图,在平面直角坐标系中,抛物线y=-
如图,在平面直角坐标系中,抛物线y=-| 2 |
| 3 |
| 4 |
| 3 |
(1)求直线BC的解析式;
(2)求抛物线的顶点及对称轴;
(3)若点Q是抛物线对称轴上的一动点,线段AQ+CQ是否存在最小值?若存在,求出点Q的坐标;若不存在,说明理由;
(4)若点P是直线BC上方的一个动点,△PBC的面积是否存在最大值?若存在,求出点P的坐标及此时△PBC的面积;若不存在,说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)令y=0,解关于x的一元二次方程求出点B的坐标,令x=0求出点C的坐标,设直线BC的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答即可;
(2)把二次函数解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;
(3)根据轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点Q,然后利用直线解析式求解即可;
(4)过点P作PD∥y轴与BC相交于点D,根据抛物线解析式与直线BC的解析式表示出PD,再根据S△PBC=S△PCD+S△PBD列式整理,然后利用二次函数最值问题解答.
(2)把二次函数解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;
(3)根据轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点Q,然后利用直线解析式求解即可;
(4)过点P作PD∥y轴与BC相交于点D,根据抛物线解析式与直线BC的解析式表示出PD,再根据S△PBC=S△PCD+S△PBD列式整理,然后利用二次函数最值问题解答.
解答:解:(1)令y=0,则-
x2+
x+2=0,
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
所以,点B的坐标为(3,0),
令x=0,则y=2,
所以,点C的坐标为(0,2),
设直线BC的解析式为y=kx+b,则
,
解得
,
所以,直线BC的解析式为y=-
x+2;
(2)∵y=-
x2+
x+2,
=-
(x2-2x+1)+2+
,
=-
(x-1)2+
,
∴顶点坐标为(1,
),
对称轴为直线x=1;
(3)由轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点,
x=1时,y=-
×1+2=
,
所以,存在Q(1,
),使线段AQ+CQ最小;
(4)如图,过点P作PD∥y轴与BC相交于点D,
则PD=(-
x2+
x+2)-(-
x+2)=-
x2+2x,
所以,S△PBC=S△PCD+S△PBD,
=
×(-
x2+2x)×3,
=-x2+3x,
=-(x-
)2+
,
所以,当x=
时,△PBC的面积最大为
,
此时,y=-
×(
)2+
×
+2=
,
所以,存在P(
,
),使S△PBC最大=
.
| 2 |
| 3 |
| 4 |
| 3 |
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
所以,点B的坐标为(3,0),
令x=0,则y=2,
所以,点C的坐标为(0,2),
设直线BC的解析式为y=kx+b,则
|
解得
|
所以,直线BC的解析式为y=-
| 2 |
| 3 |
(2)∵y=-
| 2 |
| 3 |
| 4 |
| 3 |
=-
| 2 |
| 3 |
| 2 |
| 3 |
=-
| 2 |
| 3 |
| 8 |
| 3 |
∴顶点坐标为(1,
| 8 |
| 3 |
对称轴为直线x=1;
(3)由轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点,
x=1时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
所以,存在Q(1,
| 4 |
| 3 |

(4)如图,过点P作PD∥y轴与BC相交于点D,
则PD=(-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
所以,S△PBC=S△PCD+S△PBD,
=
| 1 |
| 2 |
| 2 |
| 3 |
=-x2+3x,
=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
所以,当x=
| 3 |
| 2 |
| 9 |
| 4 |
此时,y=-
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
所以,存在P(
| 3 |
| 2 |
| 5 |
| 2 |
| 9 |
| 4 |
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点坐标的求解,待定系数法求一次函数解析式,二次函数的顶点坐标与对称轴的求法,轴对称确定最短路线问题,二次函数的最值问题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
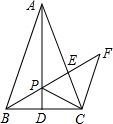 如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项.
如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项. 如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2. 如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC=
如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC=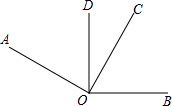 如图,∠AOC和∠BOD都是直角,∠DOC=28°,求出∠AOB的度数.
如图,∠AOC和∠BOD都是直角,∠DOC=28°,求出∠AOB的度数.