题目内容
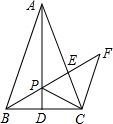 如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项.
如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项.考点:相似三角形的判定与性质
专题:
分析:首先利用三线合一定理证明∠BAD=∠CAD,然后证明△ABP≌△ACP,得到BP=PC,∠ABP=∠ACP,再证明△PCE∽△PFC,利用相似三角形的性质证得.
解答:解:∵AB=AC,BD=DC,
∴∠BAD=∠CAD,
在△ABP和△ACP中,
,
∴△ABP≌△ACP(SAS),
∴BP=PC,∠ABP=∠ACP,
∵CF∥AB,
∴∠F=∠ABP,
∴∠F=∠ACP,
又∵∠EPC=∠CPF,
∴△PCE∽△PFC,
∴
=
,即PF2=PF•PE,
又∵BP=PC,
∴BP2=PF•PE,即BP是PE、PF的比例中项.
∴∠BAD=∠CAD,
在△ABP和△ACP中,
|
∴△ABP≌△ACP(SAS),
∴BP=PC,∠ABP=∠ACP,
∵CF∥AB,
∴∠F=∠ABP,
∴∠F=∠ACP,
又∵∠EPC=∠CPF,
∴△PCE∽△PFC,
∴
| PC |
| PF |
| PE |
| PC |
又∵BP=PC,
∴BP2=PF•PE,即BP是PE、PF的比例中项.
点评:本题考查了等腰三角形三线合一定理以及相似三角形的相似的判定与性质,证明线段成比例的问题,常用方法是证明三角形相似.

练习册系列答案
相关题目
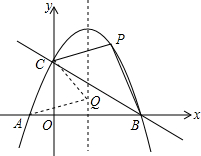 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线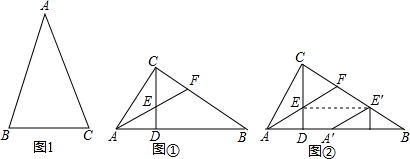
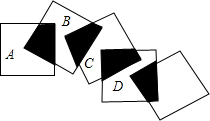 如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )
如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )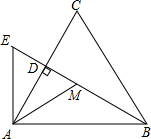 如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.
如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.