题目内容
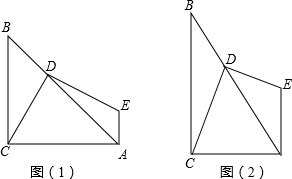
 如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2.(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.并指出当x为何值时,S有最大值.
考点:梯形,翻折变换(折叠问题)
专题:
分析:(1)根据折叠的性质即可求得BF的值;
(2)根据二次函数的最值问题可以求得S在x=-
时,有最大值,即可解题.
(2)根据二次函数的最值问题可以求得S在x=-
| b |
| 2a |
解答:解:(1)∵∠ABC=90°,DE⊥BC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是矩形,
∴AD=BE=x,AB=DE,∠DEC=90°,
∵∠C=45°,
∴∠EDC=∠C=45°,
∴DE=EC=4-x,BF=4-2x;
(2)将△DEC沿直线DE折叠,点C落在CB的延长线上F处,BC=4,BE=AD=x,
∴EC=EF=4-x,
∵AB∥DE,
∴△FBG∽△FED,
∴
=
,
S=
[(4-x)2-(4-2x)2]=
[8x-3x2],
当x=-
=
,S有最大值.
∴AB∥DE,

∵AD∥BC,
∴四边形ABED是矩形,
∴AD=BE=x,AB=DE,∠DEC=90°,
∵∠C=45°,
∴∠EDC=∠C=45°,
∴DE=EC=4-x,BF=4-2x;
(2)将△DEC沿直线DE折叠,点C落在CB的延长线上F处,BC=4,BE=AD=x,
∴EC=EF=4-x,
∵AB∥DE,
∴△FBG∽△FED,
∴
| FB |
| EF |
| 4-2x |
| 4-x |
S=
| 1 |
| 2 |
| 1 |
| 2 |
当x=-
| b |
| 2a |
| 4 |
| 3 |
点评:本题考查了相似三角形对应边比例相等的性质,考查了二次函数求最值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果a是有理数,下列各式一定为正数的是( )
| A、a+2012 |
| B、(a+1)2 |
| C、|a| |
| D、a2+1 |
如果线段a、b、c、d是成比例线段且a=3,b=6,c=5,则d=( )
| A、8 | B、12 | C、10 | D、16 |
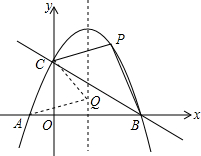 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线 已知:如图,∠C=∠D=Rt∠,AC=AD.求证:
已知:如图,∠C=∠D=Rt∠,AC=AD.求证: 已知如图:点A(0,4),B(3,0),且∠1=∠2.则C点的坐标是
已知如图:点A(0,4),B(3,0),且∠1=∠2.则C点的坐标是