题目内容
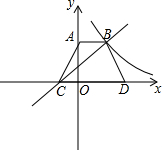 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数y=
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数y=| k |
| x |
①求一次函数与反比例函数的解析式;
②直接写出当x取何值时反比例函数值为正数且大于一次函数的值.
考点:反比例函数与一次函数的交点问题
专题:代数几何综合题,数形结合,待定系数法
分析:①过B作BE垂直于x轴,由等腰梯形ABCD,得到三角形ACO与三角形BDE全等,得到OC=ED,再由矩形AOEB确定出AB=OE,进而求出OC的长,得到C的坐标,根据BE与OE长求出B坐标,将B与C坐标代入一次函数解析式求出a与b的值,确定出一次函数解析式,将B坐标代入反比例解析式求出k的值,确定出反比例解析式;
②由B横坐标,利用图象即可确定出满足题意x的范围.
②由B横坐标,利用图象即可确定出满足题意x的范围.
解答: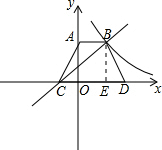 解:①过B作BE⊥x轴,与x轴交于E点,
解:①过B作BE⊥x轴,与x轴交于E点,
∵A(0,3),AB=2,
∴OA=BE=3,OE=AB=2,
∵等腰梯形ABCD,
∴∠ACD=∠BDC,AC=BD,
在Rt△ACO和Rt△BDE中,
,
∴Rt△ACO≌Rt△BDE(HL),
∴OC=ED=
(CD-AB)=1,
∵OE=2,BE=3,
∴B(2,3),C(0,-1),
将B与C坐标代入y=ax+b,得
,
解得:
,
∴一次函数解析式为y=2x-1;
将B坐标代入反比例解析式得:k=6,
∴反比例解析式为y=
;
②根据函数图象得:当0<x<2时,反比例函数值为正数且大于一次函数的值.
 解:①过B作BE⊥x轴,与x轴交于E点,
解:①过B作BE⊥x轴,与x轴交于E点,∵A(0,3),AB=2,
∴OA=BE=3,OE=AB=2,
∵等腰梯形ABCD,
∴∠ACD=∠BDC,AC=BD,
在Rt△ACO和Rt△BDE中,
|
∴Rt△ACO≌Rt△BDE(HL),
∴OC=ED=
| 1 |
| 2 |
∵OE=2,BE=3,
∴B(2,3),C(0,-1),
将B与C坐标代入y=ax+b,得
|
解得:
|
∴一次函数解析式为y=2x-1;
将B坐标代入反比例解析式得:k=6,
∴反比例解析式为y=
| 6 |
| x |
②根据函数图象得:当0<x<2时,反比例函数值为正数且大于一次函数的值.
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
下列不等式变形正确的是( )
| A、由3x-1>2得3x>1 | ||
| B、由-3x<6得x<-2 | ||
C、由
| ||
D、由4x>3得x>
|
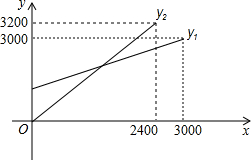 某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?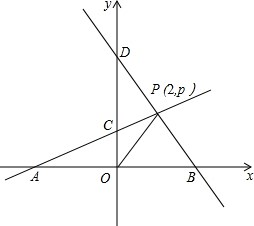 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6. 如图,直线AB、CD相交于点O.
如图,直线AB、CD相交于点O.