题目内容
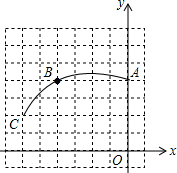 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:(1)利用网格图确定该圆弧所在圆心D点的位置(保留画图痕迹),则写出D点坐标为
(2)连结AD,CD,求⊙D的半径长为
(3)求扇形DAC是一个圆锥的侧面展开图,求该圆锥的底面半径长.(结果保留根号)
考点:圆的综合题
专题:计算题,数形结合
分析:(1)利用垂径定理得出D点位置即可;
(2)利用点的坐标结合勾股定理得出⊙D的半径长,再利用全等三角形的判定与性质得出∠ADC的度数;
(3)利用圆锥的底面圆的周长等于侧面展开图的扇形弧长即可得出答案.
(2)利用点的坐标结合勾股定理得出⊙D的半径长,再利用全等三角形的判定与性质得出∠ADC的度数;
(3)利用圆锥的底面圆的周长等于侧面展开图的扇形弧长即可得出答案.
解答: 解:(1)如图所示:D点即为所求,坐标为:(-2,0);
解:(1)如图所示:D点即为所求,坐标为:(-2,0);
故答案为:(-2,0);
(2)∵D(-2,0),A(0,4),
∴DO=2,AO=4,
∴AD=
=2
,
即⊙D的半径长为2
,
∵C(-6,2),
∴EC=2,DE=4,
在△CDE和△DAO中,
,
∴△CDE≌△DAO(SSS),
∴∠CDE=∠DAO,∠ADO=∠ECD,
∴∠CDE+∠ADO=90°,
∴ADC=90°;
故答案为:2
,90°;
(3)设圆锥的底面圆的半径为r,根据题意得出:
=2πr,
解得:r=
.
 解:(1)如图所示:D点即为所求,坐标为:(-2,0);
解:(1)如图所示:D点即为所求,坐标为:(-2,0);故答案为:(-2,0);
(2)∵D(-2,0),A(0,4),
∴DO=2,AO=4,
∴AD=
| 20 |
| 5 |
即⊙D的半径长为2
| 5 |
∵C(-6,2),
∴EC=2,DE=4,
在△CDE和△DAO中,
|
∴△CDE≌△DAO(SSS),
∴∠CDE=∠DAO,∠ADO=∠ECD,
∴∠CDE+∠ADO=90°,
∴ADC=90°;
故答案为:2
| 5 |
(3)设圆锥的底面圆的半径为r,根据题意得出:
90π×2
| ||
| 180 |
解得:r=
| ||
| 2 |
点评:此题主要考查了圆的综合以及圆锥侧面展开图以及弧长公式和全等三角形的判定与性质等知识,利用数形结合得出D点位置是解题关键.

练习册系列答案
相关题目
 在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,EF∥AC.求证:AB=BF.
在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,EF∥AC.求证:AB=BF. 在等腰梯形ABCD中,AB∥CD,AD=BC,两条对角线AC,BD互相垂直,中位线EF为8厘米,求等腰梯形ABCD过C点的高.
在等腰梯形ABCD中,AB∥CD,AD=BC,两条对角线AC,BD互相垂直,中位线EF为8厘米,求等腰梯形ABCD过C点的高.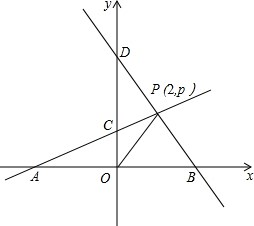 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.