题目内容
把多项式9mx4-6mx2+m在实数范围内因式分解 .
考点:实数范围内分解因式
专题:计算题,因式分解
分析:首先提取公因式m,进而利用完全平方公式以及平方差公式分解因式即可.
解答:解:9mx4-6mx2+m
=m(9x4-6x2+1),
=m(3x2-1)2,
=m(
x+1)2(
x-1)2.
故答案为:m(
x+1)2(
x-1)2.
=m(9x4-6x2+1),
=m(3x2-1)2,
=m(
| 3 |
| 3 |
故答案为:m(
| 3 |
| 3 |
点评:此题主要考查了实属范围内分解因式,熟练掌握完全平方公式和平方差公式是解题关键.

练习册系列答案
相关题目
 如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )
如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )| A、2EF=AB+CD |
| B、2EF>AB+CD |
| C、2EF<AB+CD |
| D、不确定 |
下列不等式变形正确的是( )
| A、由3x-1>2得3x>1 | ||
| B、由-3x<6得x<-2 | ||
C、由
| ||
D、由4x>3得x>
|
在下列四组数中,不是直角三角形的三边长的是( )
A、1,1,
| ||||
B、3,4,
| ||||
| C、1,2,3 | ||||
D、
|
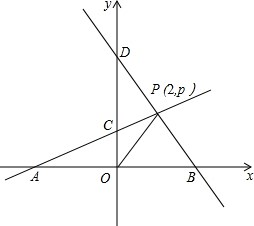 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6. 实数a、b在数轴上对应点的位置如图所示,则|b-a|-|a-b|=
实数a、b在数轴上对应点的位置如图所示,则|b-a|-|a-b|= 沿原路返回A地,返回途中行驶的速度不变,甲、乙两车在行驶途中与A地的距离S(千米)与时间t(分钟)之间的函数图象如图所示,则两车在行驶途中两次相遇的间隔时间为
沿原路返回A地,返回途中行驶的速度不变,甲、乙两车在行驶途中与A地的距离S(千米)与时间t(分钟)之间的函数图象如图所示,则两车在行驶途中两次相遇的间隔时间为