题目内容
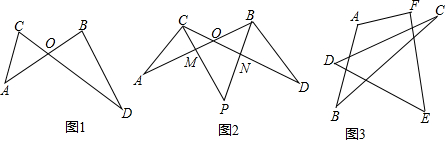
2.如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“对顶三角形”.如图2,∠ACO和∠DBO的平分线CP和BP相交于点P,并且与AB、CD分别相交于M、N.试解答下列问题:(1)仔细观察,在图2中有3个以线段OC为边的“对顶三角形”;
(2)在图2中,若∠A=40°,∠D=50°,求∠P的度数.
(3)在图2中,若设∠A=α,∠D=β,∠ACP=∠PCD,∠ABP=∠PBD,试问∠P与∠A、∠D之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360°.
分析 (1)根据“对顶三角形”的定义容易得出结果;
(2)由角平分线得出∠ACP=∠DCP,∠ABP=∠DBP,由三角形内角和定理和对顶角相等得出∠ACP+∠A=∠ABP+∠P,∠DCP+∠P=∠DBP+∠D,得出∠A-∠P=∠D-∠P,即可得出结果;
(3)由角平分线得出∠ACP=∠DCP,∠ABP=∠DBP,由三角形内角和定理和对顶角相等得出∠ACP+∠A=∠ABP+∠P,∠DCP+∠P=∠DBP+∠D,得出∠A-∠P=∠D-∠P,即可得出结论;
(4)由三角形的外角性质得出∠1=∠2+∠E,∠2=∠C+∠D,∴∠1=∠C+∠D+∠E,在四边形ABMF中,由四边形内角和即可得出结果.
解答 解:(1)在图2中有 3个以线段OC为边的“对顶三角形”;
故答案为:3;
(2)∵∠ACO和∠DBO的平分线CP和BP相交于点P,
∴∠ACP=∠DCP,∠ABP=∠DBP,
∵∠ACP+∠A=∠ABP+∠P,∠DCP+∠P=∠DBP+∠D,
∴∠A-∠P=∠D-∠P,
∴∠P=$\frac{1}{2}$(∠A+∠D),
∵∠A=40°,∠D=50°,
∴∠P=$\frac{1}{2}$(40°+50°)=45°;
(3)∠P=$\frac{1}{2}$(α+β),理由如下:
∵∠ACO和∠DBO的平分线CP和BP相交于点P,
∴∠ACP=∠DCP,∠ABP=∠DBP,
∵∠ACP+∠A=∠ABP+∠P,∠DCP+∠P=∠DBP+∠D,
∴∠A-∠P=∠D-∠P,
∴∠P=$\frac{1}{2}$(∠A+∠D),
∴∠P=$\frac{1}{2}$(α+β);
(4)如图所示:
由三角形的外角性质得:∠1=∠2+∠E,∠2=∠C+∠D,
∴∠1=∠C+∠D+∠E,
在四边形ABMF中,∠A+∠B+∠1+∠F=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
点评 本题是四边形综合题目,考查了角平分线定义、“对顶三角形”定义、三角形内角和定理、四边形内角和定理、三角形的外角性质等知识;熟练掌握三角形内角和定理和四边形内角和定理是解决问题的关键.

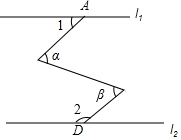 如图,直线 l1∥l2,∠α=∠β,∠1=50°,则∠2的度数为( )
如图,直线 l1∥l2,∠α=∠β,∠1=50°,则∠2的度数为( )| A. | 130° | B. | 120° | C. | 115° | D. | 100° |
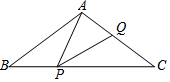 如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=3秒或$\frac{39}{8}$秒.
如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=3秒或$\frac{39}{8}$秒.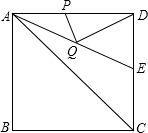 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是2$\sqrt{2}$.
如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是2$\sqrt{2}$. 已知y=-$\frac{1}{2}$x2+2x+6
已知y=-$\frac{1}{2}$x2+2x+6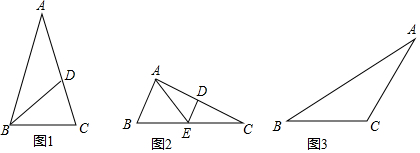
 已知如图:∠ACB=90°,AC=3,BC=4,将AC折叠后与CD重叠,BC折叠后与CD重合,求BF的长度.
已知如图:∠ACB=90°,AC=3,BC=4,将AC折叠后与CD重叠,BC折叠后与CD重合,求BF的长度.