题目内容
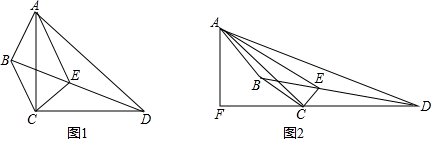
12. 已知如图:∠ACB=90°,AC=3,BC=4,将AC折叠后与CD重叠,BC折叠后与CD重合,求BF的长度.
已知如图:∠ACB=90°,AC=3,BC=4,将AC折叠后与CD重叠,BC折叠后与CD重合,求BF的长度.
分析 根据翻转变换的性质得到CD=AC=3,CB′=BC=4,∠B′=∠B,∠A=∠ADC,求出B′D=1,∠DFB′=90°,根据勾股定理计算即可.
解答 解:∵将AC折叠后与CD重叠,BC折叠后与CD重合,
则CD=AC=3,CB′=BC=4,∠B′=∠B,∠A=∠ADC,
∴B′D=4-3=1,∠DFB′=90°,
设B′F=4x,则DF=3x,
由勾股定理得,(3x)2+(4x)2=1,
解得,x=$\frac{1}{5}$,
∴BF=BF′=$\frac{4}{5}$.
点评 本题考查的是翻转变换的性质、勾股定理的应用,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列函数表达式中,y不是x的反比例函数的是( )
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{x}{3}$ | C. | y=$\frac{1}{2x}$ | D. | xy=$\frac{1}{2}$ |
7.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{{x}^{2}+1}{2}$,$\frac{3}{x+y}$,$\frac{abc}{m}$中,分式的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需$\frac{1}{3}$天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需$\frac{1}{2}$天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
表二
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |
4.$\frac{14}{3}$是( )
| A. | 整数 | B. | 无理数 | C. | 有理数 | D. | 自然数 |