题目内容
17.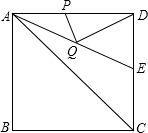 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是2$\sqrt{2}$.
如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是2$\sqrt{2}$.
分析 过D作AE的垂线交AE于F,交AC于D′,再过D′作AP′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
解答 解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2$\sqrt{2}$,
即DQ+PQ的最小值为2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了正方形的性质以及角平分线的性质和全等三角形的判定和性质和轴对称-最短路线问题,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
8.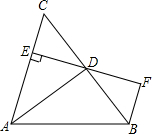 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.已知方程3x+2y=13的整数解的组数( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 无数组 |
6.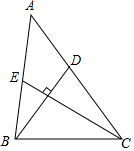 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )
 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )| A. | 12 | B. | 24 | C. | 16 | D. | 32 |
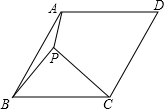 如图,菱形ABCD的边长为4,∠ABC=60°,在菱形ABCD内部有一点P,当PA+PB+PC值最小时,PB的长为$\frac{4\sqrt{3}}{3}$.
如图,菱形ABCD的边长为4,∠ABC=60°,在菱形ABCD内部有一点P,当PA+PB+PC值最小时,PB的长为$\frac{4\sqrt{3}}{3}$.