题目内容
2.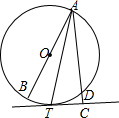 如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C
如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C(1)求证:CT为⊙O的切线;
(2)若AD=2,TC=$\sqrt{3}$,求⊙O的半径.
分析 (1)要证明PQ是⊙O的切线只要证明OT⊥PQ即可;
(2)由已知可求得OM和AM的长,从而利用勾股定理求得OA的长.
解答 证明:(1)连接OT;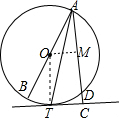
∵OT=OA,
∴∠ATO=∠OAT,
又∵∠TAC=∠BAT,
∴∠ATO=∠TAC,
∴OT∥AC;
∵AC⊥TC,
∴OT⊥TC,
∴CT是⊙O的切线.
(2)解:过点O作OM⊥AC于M,则AM=MD=$\frac{1}{2}$AD=1;
又∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,
∴OM=TC=$\sqrt{3}$,
∴在Rt△AOM中,OA=$\sqrt{A{M}^{2}+O{M}^{2}}$=$\sqrt{1+3}$=2,
∴⊙O的半径为2.
点评 本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
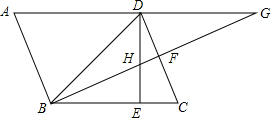 如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证:
如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证: